
(from Gk. rhythmos; Lat. rhythmus; Fr. rythme; Ger. Rhythmus; 16th-, 17th-century Eng. rithme).
Generically, a ‘movement marked by the regulated succession of strong or weak elements’ (Oxford English Dictionary). In etymological discussions of the term there is a tension between rhythm as continuously ‘flowing’ and rhythm as periodically punctuated movement. In musical contexts the term is even harder to pin down. Fassler remarks: ‘There is no accurate simple definition of the term “rhythm” (or “rhythmics”) and no consistent historical tradition to explain its significance’ (B1987, p.166 n.10). Sachs is even more pessimistic: ‘What is rhythm? The answer, I am afraid, is, so far, just – a word: a word without generally accepted meaning. Everybody believes himself entitled to usurp it for an arbitrary definition of his own. The confusion is terrifying indeed’ (A1953, p.12). Etymology is thus of little assistance.
Rhythm and pitch are the two primary parameters of musical structure (Meyer, E1973). For in specifying the tonal and rhythmic organization of a work we believe we have captured its essential structure. Changes in instrumentation, orchestration or dynamics (i.e. changes to the secondary parameters) are understood as different arrangements of the same musical work, whereas alterations in pitch or rhythm may result in a new, different work. If pitch is concerned with the disposition of the frequencies of musical notes, then rhythm is concerned with the description and understanding of their duration and durational patternings. These durations may be more or less regular, may or may not give rise to a sense of beat or tempo, and may be more or less continuous, but as all music involves duration(s), all music necessarily has some manner of rhythm. Claims that a particular piece or performance ‘lacks rhythm’ may be taken to mean that the piece or performance lacks rhythmic regularity and/or a coherent sense of motion. In a similar vein, we use the adjective ‘rhythmic’ as an aesthetic positive in describing a piece; it would be strange, for example, to say that a piece was bad because it was very rhythmic.
If ‘rhythm’ refers to patterns of duration, and if ‘rhythmic’ characterizes such a pattern as more or less regular, then the question arises as to what determines regularity. The answer is in large part the subject of §I below, but the rhythm–rhythmic distinction gives a clue as to how our definition may be further circumscribed. For a temporal pattern to be a ‘regular rhythm’ its recurrent features have to be intelligible to the human listener, and this suggests that both ‘rhythm’ and ‘rhythmic’ refer to the smaller-scale features of musical experience. There may be a deep-seated psychological reason for this, in that ‘rhythm’ may be a quality of musical figures and movement that is apprehended within the span of the perceptual present, whereas ‘form’ requires an understanding of structural relationships either wholly or partly outside the perceptual present (and thus engages one's long-term memory of the piece at hand as well as one's musical background and knowledge). While larger patterns and symmetries may occur over entire movements, days or weeks, we do not apprehend or understand these ‘rhythms’ in the way that we have a sensible, toe-tapping grasp of the periodicities present at the beginning of, for example, the finale of Haydn's ‘London’ Symphony or the Major-General's Song by Gilbert and Sullivan. The application of the terms ‘rhythm’ and ‘rhythmic’ to larger musical structures and temporal processes represents a metaphorical extension of rhythm's proper meaning.
This article is concerned primarily with musical rhythm and metre in Western music and the Western musicological tradition. Nonetheless, discussions of non-Western music and theories are noted where appropriate.
I. Fundamental concepts and terminology
II. Historical studies of rhythm
JUSTIN LONDON
The elements of rhythm are necessarily intertwined in their origin and effect. Thus, for example, while durations have certain essential properties, one's experience of duration will vary according to musical context (i.e. given the presence or absence of a regular metre). Nonetheless, this discussion begins with the duration of single notes, then proceeds to the organization of successive durations into coherent groups, the emergence of metre and metric listening, and so forth. In addition, since rhythm and metre are coherent phenomena only for a listener who can capture and remember the music as it unfolds, the following discussion engages psychological theory and research to a significant degree.
1. The distinction between rhythm and metre.
2. The perception of duration and succession.
3. Durational patterns and rhythmic groups.
4. Metre: beats, metric cycles and tempo.
5. Rhythmic and metric accent.
6. Interactions of rhythm and metre.
7. Complex rhythms and complex metres.
8. Additive versus divisive rhythm.
Rhythm, §I: Fundamental concepts & terminology
A series of events (whether musical notes or the blows of a hammer) is commonly characterized as ‘rhythmic’ if some or all of those events occur at regular time intervals. But being ‘rhythmic’ is not the same thing as being ‘a rhythm’. For a musician or musicologist ‘rhythm’ signifies a wide variety of possible patterns of musical duration, both regular and irregular. A musician is apt to observe that a regular rhythm exhibits metric properties – or, to put it directly, regular rhythms involve metre. While all music involves some type or rhythm, not all music involves metre. Thus in common usage the adjective ‘rhythmic’ often signifies what might more precisely be described as a ‘metrically regular series of events’. However, irregular rhythms can occur in the context of a regular metre (e.g. syncopated figures and asymmetrical phrase structures), and not all metres require regular or even patterns of duration (e.g. Bartók's ‘Bulgarian’ rhythms). Thus there is more to the distinction between metre and rhythm than regularity versus non-regularity.
Broadly stated, rhythm involves the pattern of durations that is phenomenally present in the music, while metre involves our perception and anticipation of such patterns. In psychological terms, rhythm involves the structure of the ‘temporal stimulus’, while metre involves our perception and cognition of such stimuli. Perhaps the earliest recognition of this distinction was made by Butler (1636; see Houle, A1987). Butler's illustration is given as ex.1; he remarked that in the top staff the minims go ‘jumping by threes’ whereas in the bottom staff they go by twos, based on the metric context established in the previous bars. That is, even if the second and third bars are performed in the same way, we will hear them differently; different perceptual attitudes give rise to different metres. As Gjerdingen (I1989) has aptly put it, ‘metre [is] a mode of attending’, while rhythm is that to which we attend.

Many of the salient differences between rhythm and metre are summarized in Table 1.

While the majority of contemporary music theorists embrace a ‘strong separation’ of rhythm and metre into separate ontological and analytical domains, not all do so. Schachter (G1987) and Rothstein (E1989) explicitly de-emphasize the rhythm–metre distinction, preferring instead to address a more general concept of ‘phrase rhythm’ (see §III, 3). Hasty (G1997) gives an especially thorough critique of this separation, drawing on the work of Friedrich Neumann (G1959). Hasty notes that the ‘strong separation’ between metre and rhythm can be traced to 19th-century theorists such as Lussy (D1885), and he also questions the basis on which rhythm and metre can interact if such a strong separation exists between them.
Rhythm, §I: Fundamental concepts & terminology
Not all durations are perceived alike, as there are a number of psycho-physical limits on our ability to perceive durations and durational succession. Hirsh (I1959) demonstrated that two onsets must be separated by at least two milliseconds (ms) in order to be distinctly perceived, and that at least 15–20ms are required to determine which onset came first. There also seems to be about a 50ms perceptual decay time – a minimum interval needed to hear one element follow another without overlap. Hirsh and others (I1990) found that 100ms seems to be the threshold for reliable judgments of length, and Roederer (I1995) noted that 100ms seems to be a threshold for processing in the cerebral cortex, and is thus the minimum duration that engages a ‘musical’ (i.e. learnt) understanding of sound and constructs such as scale degrees and rhythmic archetypes. The maximum interval for reliable estimates of the length of single durations, as well as for the connection of successive articulations, is usually 1·5–2·0 seconds. This limit is related to the limitations of short-term memory and the perceptual present (Fraisse, I1978; Handel, I1989). Musicians and musicologists have long been aware of these upper and lower bounds, as they appear in the context of discussions of tempo and performance limits (see, for example, Westergaard, E1975).
Just as there are perceptual and cognitive biases and constraints on our understanding of duration, there are also similar constraints on our apprehension of musical texture, some of which impinge on our understanding of rhythm. In perceptual psychology texture is investigated under the rubric of ‘auditory streams’ which are the ‘perceptual grouping(s) of the parts of the neural spectrogram that go together’ (Bregman, I1990). It is through the process of auditory streaming that we are able to pick out some sounds in our environment and hear them as connected and coherent, whether they are a single voice in a crowded room or a single part in a complex musical texture. Research in auditory streaming has shown that pitch, tempo, timbre and loudness are all factors that affect our ability to segregate sounds into separate streams. Some streaming effects interact with our perception of duration; for example, Van Noorden (I1975) has shown that when two isochronous streams cross, an uneven (‘galloping’) rhythm is nonetheless perceived. It is through streaming that we are able to hear compound melodies, and hence perceive a series of different durations within a musical surface consisting of even articulations, as in ex.2.

Along with streaming effects, other factors can influence our perception of duration. As summarized by Handel (I1989), intensity and/or pitch differences between evenly spaced notes tend to be heard as durational differences (with a longer duration perceived from the onset of the unstressed or lower note to stressed or higher note, and vice versa). Similarly, durational differences may be perceived as differences in intensity or loudness, and the durational and/or intensity difference(s) of one note may interfere with durational judgments of other notes. Repp (I1995–6) has reported that in metric contexts listeners expect slight variations in duration, such that actual durational differences may go unnoticed if they occur where they are expected, or may seem exaggerated if they occur in unexpected metric positions.
Musical durations (and hence rhythmic groups) are almost exclusively recognized from note onset to onset. Ex.3 contains three different musical figures: (a) a series of staccato notes; (b) a series of legato notes; and (c) an arpeggio. While 3a and 3b differ with respect to the absolute value of their component notes, and while 3c is texturally different from 3a and 3b, all three express the ‘same’ rhythmic pattern – a three-element series with a sense of accent on the first element (prosodically, a dactyl). While rests between sounds may be salient, most often they inform the perceived quality of articulation (i.e. staccato versus legato) rather than being heard as musical objects in themselves (except that in established metric contexts some rests can be heard as having definite duration: see London, G1993).

See also Hearing and psychoacoustics and Psychology of music, §II, 2.
Rhythm, §I: Fundamental concepts & terminology
As James noted, ‘To be conscious of a time interval at all is one thing; to tell whether it be shorter or longer than another interval is a different thing’ (I1890, p.615). Metre obviously plays a crucial role in the determination of relative duration. Nonetheless, we are also aware of relative durations in non-metric contexts. The first judgment to be made regarding two successive durations is whether they are the same or different. This distinction is not as trivial as one might suppose. Within the range of rhythmic acuity described above, the perception of duration follows a modified form of Weber's law, in which the just-noticeable difference between two successive durations is proportional to their absolute length (plus a constant of minimal discrimination: see Allan, I1979). There are also effects of ordering (whether the longer note comes first or last), pitch proximity and differences in loudness, all of which influence durational comparisons. If two successive durations are judged as different, then their difference can be conceived and represented in different ways. One may simply compare the first interval with the second, using the first as a sort of temporal yardstick. This strategy may be used when the two durations are close to each other in length. If the two durations differ to a greater degree, rather than comparing the second directly with the first, one may relate each to previously established perceptual categories of duration. These categories may simply be ‘long’ versus ‘short’, or they may be more nuanced (e.g. ‘very long’, ‘long’, ‘medium’, ‘short’, ‘very short’). Such categorical perception of duration has been documented in psychological studies, and it does not require precise (i.e. proportional) definition of the respective categories (see Clarke, I1987).
Two or more musical durations may cohere into a larger unit, termed a ‘rhythmic group’. The creation of coherent, well-articulated rhythmic groups is one of the principal tasks the performer faces in realizing a musical score: to project a sense that some notes go with other notes, and that these groups themselves form larger units. From this process the basic musical shapes of a piece may be discerned.
In the absence of phenomenal cues for group boundaries we will arbitrarily impose a sense of group structure on a series of events. 18th-century theorists such as Koch (1787) noted this propensity (see discussion in Hasty, G1997), and in 20th-century psychological studies this is known as ‘subjective rhythmization’ (Fraisse, in Action and Perception, I1985; Handel, I1989). The two principal factors that influence group boundaries are proximity and similarity (see Meyer, I1956; Lerdahl and Jackendoff, E1983; Handel, I1989; and Bregman, I1990). In ex.4a proximity (as well as placement on a common horizontal line or pitch plane) gives the sense that the series of Xs or notes is organized into three groups of three. Composers, copyists and engravers have long understood the importance of note-spacing in projecting a sense of group boundaries. It can be seen that this proximity is marked from note onset to note onset. In an analogous case which employed a continuous series of durations (e.g. two crotchets plus a semibreve) we would find the same grouping structure. Small variations in onset timing may have an impact on proximity judgments (and hence grouping structure); the common performing practice of taking extra time for bowing or breathing following longer notes exploits (and underscores) our innate proclivity to hear a long note as the end of a group (see Gabrielsson, H1988). Ex.4b illustrates the effect of similarity on the perception of group boundaries. Even though the pitches are equally spaced in this example, one again perceives a series of triplets. In ex.4c the effects of similarity and proximity are combined. As can be seen, proximity is of greater salience than similarity, for despite the sharp differentiation of pitch, the differentiation of note-onset proximities creates a series of four-element groups. Group boundaries can be marked by changes in any musical parameter, including dynamics, timbre and texture. However, grouping is primarily marked by patterns of duration and timing, with pitch playing an important, though secondary role (see §III, 6).

Once the boundaries of a group have been established one may describe its internal structure, though often these two issues are interdependent. Cooper and Meyer (E1960), whose prosodic approach to musical rhythm has its antecedents in 17th- and 18th-century discussions of rhythmopoeia such as those of Mersenne (MersenneHU) and Mattheson (C1739), begin with a list of two or three-element archetypes for musical groups; these involve the relationship between one accented and one or two unaccented elements in each group (iamb, trochee, dactyl, anapest and amphibrach). Cooper and Meyer then consider each archetype in various metric contexts. Lerdahl and Jackendoff (E1983) do not employ durational archetypes in their analysis of rhythmic grouping; rather, they focus on the determination of group boundaries and on the hierarchical nesting of subgroups. In Lerdahl and Jackendoff's theory the internal structure of each group is determined by the interaction of metrical and tonal components (see §III, 3).
The same pattern of pitches and/or durations may allow for more than one grouping interpretation (see ex.5). These various groupings may be differentiated compositionally (for example, by the patterning of the accompaniment) or by articulative and dynamic cues in performance. The fact that the same pattern of pitches and durations may give rise to different grouping (as well as metric) structures has implications for the historical study of rhythmic notation and performance. Rhythmic notation must somehow inform the performer how to make rhythmic nuances in performance, either with explicit markings, with hints from spacing and orthography, or through shared conventions of score interpretation (e.g. metre as an indication of bowing and hence grouping, characteristic styles of rhythmic performance for various dance genres, and so forth).

Rhythmic groups may be nested hierarchically, and thus smaller groups may function as composite elements within a larger group. Ex.6 consists of a pair of simple dactylic groups, while in ex.6b the dactyls are themselves composed of trochaic subgroups. One reason we are able to hear ex.6b as a variant of ex.6a is that we treat the grouping structures as commensurate; the elaborations in ex.6b, while adding extra depth to the rhythmic hierarchy, do not alter the basic rhythmic pattern on the crotchet level.
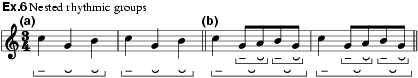
Rhythm, §I: Fundamental concepts & terminology
Metre is a structured attending to time which allows the listener to have precise expectations as to when subsequent musical events are going to occur. Dowling, Lung and Herrbold (I1987) have studied and described such directed attention in terms of ‘expectancy windows’; Jones and her colleagues (I1981, 1989, 1990, 1995, 1997) have given considerable attention to the process of entrainment, whereby one synchronizes one's attention to regular patterns of information present in the environment. Musical metre, then, would seem to be a particular utilization of our more general capacities for temporal perception. Thus, while knowing that waltzes are in triple metre tells us something (at least in broad terms) about their rhythmic structure, it also tells us even more about the way we listen to and/or perform them.
First and foremost, metre requires an awareness of a beat or pulse. A series of very rapid notes (such as a sustained tremolo) does not give rise to a sense of metre, nor does a series of very long or widely spaced notes. Only when we hear a series of regular articulations in a certain range (from 100ms to 2 seconds apart) does a sense of pulse arise. More familiarly, a 2-second duration is a semibreve at a tempo of crotchet = 120 (the upper limit), while a 100ms duration is a semiquaver at a tempo of crotchet = 150 (the lower limit). While these very short and rather long durations may constitute individual levels of a metric hierarchy, they are at the ends of the metric spectrum. Psychological research has validated what musicians have long known: we have a preference for tempos within a narrower subrange of these extremes (see also Psychology of music, §II). Parncutt (I1993–4) has examined a range of ‘maximal pulse salience’ (from 60 to 150 beats per minute, anchored at approximately 100 beats per minute) wherein pulses tend to be most strongly felt. Our sense of tempo is not simply based on the shortest (or longest) durations present in the musical surface, though such durations contribute to the particular quality of motion present, such as a ‘tense’ adagio or a ‘serene’ allegro. As Epstein (H1995) notes, tempo is an aggregate effect of the total metric hierarchy – its relative depth, the continuity of its various levels and so on.
The perception of a beat or pulse is not only necessary for a sense of ‘connectedness’ among successive events; it may also be necessary for a sense of motion, a temporal/auditory analogue of the ‘phi phenomenon’ in visual perception (Wertheimer, I1912; Bregman, I1990). The special salience of the pulse level has been acknowledged in various theoretical models of metre, from Cooper and Meyer's ‘primary rhythmic level’ (E1960, p.2) to Lerdahl and Jackendoff's ‘tactus’ (E1983, p.71). If the beat level should drop out, we immediately feel suspended in time and await its restoration.
A sense of beat, while necessary, is not sufficient to engender a sense of metre. Another layer of organization is also required, giving rise to a metric hierarchy which contains two or more coordinated levels of motion. Koch (D1782–93, ii) recognized beats (Taktteile) as primary components of the measure (Takt), while various subdivisions (Taktglieder and Taktnoten) are produced by analogous partitions of the beat. Weber (D1817–21), with an emphasis on symmetry as an organizing principle, noted that
Just as beats together form small groups, several groups can also appear bound together as beats of a larger group, of a larger or higher rhythm, a rhythm of a higher order. One can go even further and place such a rhythm of a higher order with a similar one, or a third, so that these two or three together form yet a higher rhythm. (1824, pp.102–3; trans. from Morgan, E1978, p.437)
Thus Weber extended metric relationships both upward and downward, as opposed to earlier theorists who began with the measure and then proceeded by division. Similar descriptions can be found in Hauptmann (D1853), who spoke of ‘metric construction inwards and outwards’, as well as Riemann (D1903–4), who articulated the principle of Achttaktigkeit to describe an eight-measure metric schema (see also Klages, E1934; Leichtentritt, E1951).
Given the emphasis on symmetry and the pervasiveness of the systole/diastole metaphor for musical motion, 19th-century accounts of metre were strongly biassed towards binary principles of metric organization. Present-day theorists continue the hierarchic approach to metric structure but have relaxed the strictures on its organization. Cooper and Meyer define metre as ‘the measurement of the number of pulses between more or less regularly recurring accents’ (E1960, p.4). Yeston describes metre as the interaction between two adjacent levels of motion (E1976, p.67). Lerdahl and Jackendoff note that ‘fundamental to the idea of meter is the notion of periodic alternation of strong and weak beats’ and that ‘for beats to be strong or weak there must exist a metrical hierarchy – two or more levels of beats’ (E1983, p.19). They go on to specify how the metric hierarchy must be organized through a series of metric well-formedness rules. These rules work in a bottom-up fashion, prescribing that beats come in twos or threes and that beats and measures be isochronously spaced. Kramer (K1988) relaxes these constraints and allows for the non-isochronous spacing of beats and hyperbeats (though they still must occur in cycles of twos or threes).
While two levels of structure will give rise to a sense of metre, most metric hierarchies are more richly organized. Time signatures used in Western notation since the 17th century specify four basic metric types, based not only on the organization of each measure into two or three beats, but also on the organization of beat subdivisions into duplets or triplets (see Table 1). These time signatures specify three levels of structure and thus define the pacing of rapid, moderate and slower events in a coordinated fashion. Additional subordinate and superordinate levels of organization are possible. Subdivisions are constrained by our abilities to discriminate among rapid stimuli, as individual note onsets become a perceptual blur (as in rapid sweeps in Chopin). Limits on superordinate levels are more controversial. Clearly there may be a sense of attending above the measure (see Caplin, D1981, on ‘notated versus expressed’ metres), but the extent of such ‘hypermetres’ remains a topic of considerable debate (see §III, 1).
The beat level of the metric hierarchy serves as the temporal anchor for the other levels. Thus neither a ‘top-down’ approach (where one starts with the duration of an entire measure or larger unit and then proceeds to partition that span into beats, and those beats into subdivisions) nor a ‘bottom-up’ approach (where one starts with the shortest durations present on the musical surface, combines them into beats, and those beats into measures and so forth) is quite right. Rather, a sort of ‘middle-out’ perspective on metre seems most consonant with the way we attend to (as well as represent) rhythmic events. For higher and lower levels may come and go over the course of a piece without breaking its temporal thread; a layer of subdivision may be absent entirely, or freely change from duplets to triplets without perturbing our sense of temporal continuity. Ex.7 illustrates how the number of metric levels may fluctuate over the course of the piece, from two or three above and below the beat in the opening bars (ex.7a) to its distillation down to simple pairs of beats (ex.7b). (Here and elsewhere, layers of dots under the staff correspond to levels of the metric hierarchy. A metric event is more or less accented depending upon the number of levels on which it occurs, indicated by the greater number of vertically aligned dots under that event.) In a very real sense these fluctuations are changes of metre, as they represent changes in the degree and depth to which the listener is entrained to the music.

Finally, if metre is a complex mode of musical attending, in characterizing a piece or passage as ‘metric’ one usually means that composer, performer and listener all share the same temporal perception(s) of the music. If a performer maintains a complex counting framework in the execution of a musical work, but this framework is aurally inaccessible to the listener, then that musical work is not metric in the ordinary sense. If the performer maintains one sense of metre while the listener infers another (which may be possible in a wide variety of contexts), then the music is metric but in a multivalent sense. If on the other hand the performer maintains one sense of metre but the listener is unable to infer any sense of metric organization at all, then the music is in some sense non-metric. Thus the presence of metric notation (whether in Babbitt or Baude Cordier) does not guarantee the presence of a metre (see §II, 4).
Rhythm, §I: Fundamental concepts & terminology
Perhaps the thorniest problem in discussing rhythm and metre involves their respective accents. In its broadest sense, ‘accent’ is a means of differentiating events and thus giving them a sense of shape or organization. Many sources distinguish between ‘qualitative’ and ‘quantitative’ accent. These terms originated in discussions of poetry and linguistic accent, and were subsequently applied to music. Originally, qualitative accent referred to poetic rhythms whose elements were differentiated by dynamic or intonation stress, as distinct from those differentiated by length. This opposition in turn informs the distinction that has been made between stress-timed and syllable-timed languages. Yet, as Handel (I1989) notes, all languages employ both qualitative and quantitative accents. Moreover, from a perceptual point of view quantitative differences result in qualitative distinctions, and conversely qualitative distinctions are often perceived not simply as, for example, difference in dynamic emphasis, but also as differences in duration.
A metric accent marks one beat in a series as especially strong or salient, such that it functions as a downbeat, while a rhythmic accent makes one element in a series of durations the focal member of the rhythmic group. Cooper and Meyer, in recognizing the difficulty of pinning down rhythmic and metric accent, simply said that an accent event is ‘marked for consciousness in some way’ (E1960, p.8). They distinguished accent from stress, which is the ‘dynamic intensification of a beat, whether accented or unaccented’. Thus, for example, the dynamic and textural emphasis that occurs on the second beat of each bar in a mazurka does not displace the downbeat (and hence the sense of metric accent).
The relationship between tonal motion and rhythmic and metric accent(s) has generated a considerable amount of discussion, much of it focussing on the accentual status of cadences and other components of phrase structure (for a summary see Kramer, K1988). Analyses of rhythm and metre by Schenkerian theorists, most notably in the work of Schachter (E1976, E1980, G1987) and Rothstein (E1989), engage analogous concerns. Not surprisingly, from a Schenkerian perspective rhythmic accent is generated via top-down linear processes, as it derives from tonal motions which serve to articulate various structural levels. Schachter (G1987) also notes that metric accent accrues to the boundary points of various time spans, and that such spans may be articulated by both durational and tonal processes. Rothstein, drawing on the work of Koch (D1782–93) and Schachter, posits that middleground tonal motions are inherently regular, based on symmetrical archetypes which may be modified or transformed in the foreground. Rothstein also emphasizes the ways in which rhythmic groups and metric structures tend to be commingled, and so approaches questions of metre and accent through a consideration of ‘phrase rhythm’ which includes both metrical and rhythmic components (see also §III, 2).
Other theorists consider accent by focussing on musical motion and on those points which serve as crucial moments in its ebb and flow. This perspective naturally leads to considerations of metre and metric accent. Momigny (D1803–6) spoke of an upbeat-downbeat motion (from levé to frappé) which inheres at both foreground and higher levels. A similar account of arsis and thesis was given by Riemann (D1903–4), who integrated a recursively applied concept of upbeat-to-downbeat into an eight-bar metric/rhythmic schema. Zuckerkandl (G1956) developed a wave model of metre, linking successive upbeat and downbeat motions:
With every measure we go through the succession of phases characteristic of wave motion: subsidence from the wave crest, reversal of motion in the wave trough, ascent toward a new crest, attainment of a summit, which immediately turns into a new subsidence. … Our sympathetic oscillation with the metre is a sympathetic oscillation with this wave. (p.168)
The crest of the metric wave is a point of metric accent, a moment of beginning. The correlation between a point of beginning and metric accent has been explored by Berry (G1976), who speaks of ‘reactive’ and ‘anticipative’ impulses and their corresponding accents; this parallels Zuckerkandl's account of motion from trough to crest (see also Brower, E1993). Kramer similarly defines metric accent as ‘a point of initiation’ (K1988, p.86). Benjamin (G1984), drawing on the work of Berry, attempts to quantify and tabulate various factors (harmonic change, relative stability, relative dissonance, contour, textural density and so forth) which mark such points of initiation and thus define accent algorithmically; Lester (E1986) espouses a similar approach.
Other theorists have refined Cooper and Meyer's distinction between accent and stress. Epstein distinguishes stress, rhythmic accent and metric accent. He places metre and rhythm into separate temporal domains, a ‘chronometric time’ consisting of beats and metric accents, and an ‘integral time’ which contains pulses and rhythmic groups (E1979, pp.58–62; see also Souvtchinsky, K1939). Lerdahl and Jackendoff distinguish three varieties of accent: phenomenal accents which ‘give emphasis or stress to a moment in the musical flow … such as sforzandi, sudden changes in dynamics or timbre, long notes, leaps … and so forth’, structural accents which are ‘caused by melodic/harmonic points of gravity in a phrase or section’, and metrical accents which accrue to a ‘beat that is relatively strong in its metrical context’ (E1983, p.17). Their metric accent is hierarchic in nature, in that a metrically accented event on one level is also present on higher levels; these relationships are indicated by their dot notation which marks the emergent metric grid. In Lerdahl and Jackendoff's approach metre is read in relation to grouping structure, though it is restricted to a few levels in the musical foreground (see §III, 2). This hierarchic approach to metric accent has its precursors in Komar (E1971) and Yeston (E1976) and is also adopted by Kramer (K1988).
Rhythm, §I: Fundamental concepts & terminology
The first question to consider in discussions of rhythm-metre interaction is, ‘Which comes first, rhythm or metre?’. Hauptmann (D1853), for example, viewed metre and metric processes as prior to rhythm, while Neumann (G1959) takes the opposite view. Metric priority implies that durational patterns are understood only within the context of a metric framework (and, on some views, are generated from that framework; see Johnson-Laird, I1991). The pulse train which is the substrate of metre may be internal to the listener, or it may be given in the music, but in either case rhythmic shapes gain their identity in relation to it. Conversely, from the point of view of rhythmic priority, the metric framework is inferred from the unfolding durations; Lerdahl and Jackendoff (E1983) give a formalized treatment of such a metric discovery process. On this view it also follows that metre is not inherently regular, given that it flows from the fluctuating stream of durations. Rather, metricity lies in the listener's sense of temporal comparison or measurement. At the root of the question of rhythmic or metric priority are fundamentally different conceptions of time and temporal consciousness (for a discussion of the historical and philosophical aspects of this issue, see Hasty, G1997).
One may steer a middle course between these two perspectives. When a piece begins, its metre and tempo are usually not known to the listener, and so the listener must make metric inferences (usually quickly and without difficulty) from the pattern of durations and stresses that are given. Once the metre is established it takes on a life of its own; the listener may then project a sense of accent on to an event even if it is not otherwise marked by duration, dynamics, contour or harmonic change. Thus at some times a sense of accent flows from the musical surface to the emerging metre, and at other times from the metre to the unfolding musical surface. Metre is not constant over the course of a piece, and should the metre falter or collapse later on, the listener must again seek an appropriate metric framework.
We often speak of conflicts between rhythm and metre. As Hasty has rightly observed, ‘to enter into conflict metre and rhythm must share some common ground’ (G1997, p.17). In hearing metrically, a listener also generates a series of rhythmic groups, a pattern of durations and rhythmic accents. Thus two grouping patterns are usually present in the musical experience: that expressed by the musical surface, and that generated by the metrically entrained listener. While often these patterns are perfectly congruent (see ex.8a), quite often they are not (ex.8b). In Beethoven's ‘Ode to Joy’ there is a one-to-one correspondence between rhythmic and metric events, and both measures and groups have their boundaries in the same locations. In the Haydn example, however (ex.8b), the rhythmic groups in the first violin part have a different number of elements from the metre (which is clearly expressed by the other members of the quartet, who play a foursquare accompaniment in quavers), and these groups are offset from the metric boundaries because of anacrustic figures. Nonetheless, in ex.8b these groups are coordinated in a number of important ways. Both the ‘rhythmic group’ and the ‘metric group’ express the same length. It may also be observed that in both examples the rhythmic and metric accents coincide – the downbeats of each bar are also the location for the note which functions as the focal note in each group. In other words, though groups and measures are non-congruent in ex.8b, the result is not a polyrhythm or polymetre.

More serious conflicts occur in the cases of syncopation and hemiola (ex.9). Yeston (E1976) and Krebs (G1987), building on the work of Sachs (A1953), have described these conflicts in terms of ‘metric dissonance’, and their approach has been taken up by theorists such as Rothstein (E1989), Cohn (G1992, G1992–3), Kamien (G1993) and Grave (G1995). Metric dissonances occur when secondary accents and/or group lengths undermine the established metre to the point that a secondary metric framework may emerge; in ex.9a Holst's melody refuses to settle into the 2/4 framework, but neither can it quite establish a new metre. In ex.9b, however, there is a local shift of metre, from compound duple to simple triple in the second and fourth bars. Note in this case that the quaver and dotted minim levels of metre remain the same; the shift occurs only on the beat level (from dotted crotchets to crotchets and vice versa).
Polyrhythms entail even greater complexity, as they involve the simultaneous (as opposed to successive) presence of two different rhythmic or metric streams. Thus, for example, if the bass line in ex.9b maintained the 6/8 metre while the upper part shifted to 3/4, the result would be a true polyrhythm. Polyrhythms are often described in terms of the presence of two (or more) concurrent metres (thus, more properly, polymetres); descriptions of metric dissonance often make similar assumptions. However, work in perception of polyrhythms (Lashley, I1951; Handel and Oshinsky, I1981; Handel, I1989; Klapp and others, I1985; Grieshaber, I1990; and Jones and others, I1995) suggests that we are unable to hear two metric frameworks at the same time, but either hear polyrhythms in terms of a dominant metre, or construct a composite metre to accommodate both rhythmic streams.

A number of theorists (Cone, E1968; Westergaard, E1975; Benjamin, G1984; Schachter, E1976; Berry, G1976; Komar, E1971; and Lerdahl and Jackendoff, E1983, summarized in Kramer, K1988) have concerned themselves with the relationship between phrase structure and metre or, more precisely, hypermetre. Here the chief concern is the alignment between the tonal structure of a phrase and the accentual organization of the hypermeasure, especially with respect to the interaction(s) between cadences and hypermetric accent. A related concern is whether the tonal structure of the phrase determines the higher-level metric accent or vice versa (see §III, 1).
Rhythm, §I: Fundamental concepts & terminology
While complexities such as hemiola and syncopation may arise from the interactions between rhythm and metre, rhythmic and metric structures may also exhibit considerable complexity in their own right. In describing either a measure or a rhythmic group one may note (a) its overall size, in terms of both its absolute duration and the number of elements it contains; (b) the number of structural levels it comprises; (c) the variety of its elements (e.g. the range of durational values within it); and (d) the degree of redundancy in its organization. These factors must be considered together, for a large number or variety of elements does not in and of itself entail rhythmic or metric complexity. For instance, ex.10 contains many notes and many levels of metric structure, yet it is not rhythmically or metrically complex, given the high degree of redundancy in its grouping and metric structure.

More complex rhythms involve a variety of contrasting durational values. In ex.11 there is alternation between a series of short durations and then an extremely long inter-onset interval between groups. As the metric subdivisions (and indeed almost the beats themselves) lapse during the grand pauses, the result is both an indeterminacy with respect to the ‘end’ of each group and a sense of discontinuity between successive metric units. Ambiguity of group organization and/or boundaries adds to rhythmic complexity. In ex.12 the sense of closure and group articulation that occurs on the second beat of bar 4 is undermined by the sequential repetition of the motif in bars 5–6; the result is a sense that bars 3–6 form a group in their own right, blurring the cadence in bar 4.


Complex metres involve irregular relationships among elements on a single metric level as well as between adjacent levels (Jones and Boltz, I1989). The hallmark of complex metres is that some levels are non-isochronous. In ex.13a, showing a metre commonly referred to as mixed or alternating, the downbeats are unevenly spaced, but regularity occurs every five beats. In ex.13b the quavers are too rapid to be felt as beats, and the result is a series of uneven beats with a ratio of 2:2:2:3. Such 2:3 ratios for the duration of successive beats are characteristic of metres with complex beat patterns and give the music its ‘limping’ quality (see Brăiloiu, J1951, on ‘aksak’ rhythm). Complex metres typically are indicated with a fractional time signature such as 2+2+2+3/8. Complex metres also tend to be more fragile, in that they readily devolve into metres with isochronous beat or measure periods, and in that only a limited range of durational patterns is possible in any given complex metre. Subdivision is also usually explicitly present to ensure the intelligibility of the metre.

On a larger scale, the use of constantly changing patterns of rhythm and/or shifting metres adds another level of structural complexity. Elliott Carter has developed and described the technique of ‘metric modulation’, which he uses in his percussion piece Canaries (ex.14). Of this excerpt Carter writes that ‘to the listener, this passage should sound as if the left hand keeps up a steady beat throughout the passage … while the right-hand part, made up of F-natural and C-sharp, goes through a series of metric modulations, increasing its speed a little at each change’ (F1977, p.349). Canaries has its antecedents in the use of a series of proportional changes in mensuration in pre-tonal music.

Rhythm, §I: Fundamental concepts & terminology
In discussions of rhythmic notation, practice or style, few terms are as confusing or used as confusedly as ‘additive’ and ‘divisive’. Additive rhythms are said to be produced by the concatenation of a series of units, such as a rhythm in 5/8 which is produced by the regular alternation of (2/8 + 3/8). Divisive (or, more often, multiplicative) rhythms are produced by multiplying some integer unit such that a measure of 2/4 is equal to 2 × 2/8. In addition, additive is associated with asymmetrical rhythms, while divisive rhythms are often assumed to be symmetrical. As a result, the first problems that often arise occur in the case of triple metres, which can be regarded as divisive (e.g. 3/4 = 3 × 1/4) but often involve the pairing of unequal durations (e.g. a minim plus a crotchet, creating a 2/4 + 1/4 figure, to put it in appropriately metric terms; see Rastall, A1982). While this problem stems from a conflation of metric beats with rhythmic durations, deeper confusions regarding additive versus divisive rhythm also occur.
These confusions stem from two misapprehensions. The first is a failure to distinguish between systems of notation (which may have both additive and divisive aspects) and the music notated under such a system. The second involves a failure to understand the divisive and additive aspects of metre itself. Few notational systems are wholly additive or wholly divisive, given the practical problems such systems create (see §II, 1). Any notational system that uses different orthographic forms (or patterns of forms, in the case of modal rhythm) for different durations will have to define their interrelationships in some way, and this is almost universally done in terms of proportional differences between different shapes. Therefore, on a note-to-note level successive durations will be expressed in terms of some multiplicative or divisive relationship (e.g. that a given note is half or twice as long as the note that preceded it). Yet ‘additive’ and ‘divisive’ mean more than simple note-to-note durational relationships, in that they imply the manner in which a series of durations coheres into a larger figure. Additive rhythms are constructed and understood from the ‘bottom up’, while divisive rhythms are constructed and understood from the ‘top down’. Additive and divisive are therefore claims about the essential nature of the rhythmic hierarchy in a particular piece or style.
Notational systems that are metrically equivocal tend to give representations of durational sequences that are neither specifically additive nor divisive. For example, while there is a divisive aspect to modal rhythm, in that one must see the entire ordo in order to understand which mode is present, this is not the same as understanding shorter durations in terms of their generation from longer spans via some process of division. Later Franconian and Petronian refinements of modal practice, while giving greater precision and flexibility, essentially remain systems representing a linear series of durations. Such notational systems do not express any hierarchical structure of either an additive or a divisive nature. This is not to say that the music written in modal notation cannot contain hierarchical rhythm; one would be hard pressed to claim that pieces which employed primarily 3rd- or 4th-mode rhythms do not project a sense of metre akin to compound duple time. Conversely, just because a notational system is hierarchic (i.e. divisive), it does not follow that the musical rhythms notated under such a system are (see ex.14 above).
Metre itself contains additive and divisive components, and this suggests that our understanding of rhythm in general involves both additive and divisive aspects. Psychological studies of metre indicate that above the level of the beat all metres are additive: 2/4 (1+1), 3/4 (1+1+1) and so forth. On the other hand, below the level of the beat metric and rhythmic relationships are usually divisive, in that these shorter durations are given definition through the subdivision of the beat in simple metres (see Shaffer, H1982). Standard metric pedagogy and practice reveal this basic distinction between beats and subdivisions: one counts a basic frame additively (‘1 2 3, 1 2 3 …’) and then interpolates subdivisions within it (‘1 and 2 and 3 e-and-uh, 1 2 and-uh 3 and …’). For this reason, metric subdivision can come and go over the course of a passage, and even shift from duple to triple without seriously disturbing the sense of metre. Complex metres differ from simple metres in that the units of addition, rather than simple isochronous beats, are nested ‘packets’ of shorter durations which themselves define long versus short beats. While this means that in complex metres the listener's sense of the subdivision cannot come and go (which may account in large part for the qualitative differences between simple and complex metres), the counting process in complex metres remains analogous to the counting of rapid subdivision in simple metres.
A history of rhythmic practice in Western music is tantamount to the history of Western music itself. Therefore, this section will not attempt to present a historical survey of rhythm (Western or otherwise). Rather, the advent of modal rhythm at the end of the 12th century and the shift to ‘modern’ rhythmic and metric notation around the turn of the 17th century will serve as touchstones for discussing a number of issues relating to the historical evolution of rhythmic theory and practice. Every musical culture and style must define for its practitioners what patterns of duration are to be played, how fast they should go, how the various parts of an ensemble are to be coordinated and so forth. In so doing, every culture is constrained by its literacy, its language, its conceptions of time and motion, prior musical practice, and the basic capacities of human memory and rhythmic behaviour.
See also Analysis; Conducting; Notation; Rhythmic modes; and Tempo and expression marks.
1. Basic constraints on rhythmic notation.
2. Rhythm in language and rhythm in music.
3. Synchronization and coordination of multi-part textures.
4. The ‘metre revolution’ c1600.
Rhythm, §II: Historical studies of rhythm
The history of rhythm in Western music is bound up with the history of Western musical notation, since it is principally through the evolution of notation that we may understand the constants and variables of changing rhythmic theory and practice. Musical notation may fulfil various functions (see Rastall, A1982): as an aide-mémoire for music whose structure and manner of performance are already known to the musician; as a representation, to a greater or lesser degree, of the musical structure that is to be performed; and as representations of actual performances (such as the transcription of a jazz solo or the MIDI files from a performance on a MIDI instrument). While the first type of notation usually leaves many details of rhythm unspecified (often to the frustration of the musicologist or performer), the last can be equally frustrating in its exactness. A rhythmic structure is an archetype that can be instantiated by different performers on various occasions. The rhythmic ‘structure’ that we seek to find and explain is thus always a set of relationships between various musical parameters, rather than a specific series of durations, intensity levels and so forth.
At first glance, many systems of rhythmic notation seem more complex than necessary. For all that a logically coherent and exhaustive system of rhythmic notation requires is three basic symbols: an atomic durational unit (i.e. a chronos protos), a rest of equal duration and a ligature to bind the notes or rests together into units of greater value. Such a system allows for the notation of any durational sequence or proportion, provided the atomic durational unit is the smallest common factor of the various durations present in the music. For pieces that use a limited range of durational values such a system is adequate, and indeed such systems have occasionally been in use (e.g. ‘stroke’ or ‘strene’ notation). But in passages of even moderate rhythmic complexity such a system of duration is unworkable for practical reasons. While exx.15a and 15b accurately express the same durational sequence, ex.15a is almost unintelligible, though perhaps the durational values of tied notes could be made clearer by altering their spacing. Also, while the stroke notation may be workable for monophonic music, in a polyphonic context it is difficult, if not impossible, to indicate the coordination of parts clearly. Thus as a rule the orthography of a notational system must be broad enough to capture the range of durational values in use in a particular style, yet specific enough to represent categorically distinct durational figures. Linking differences in duration to differences in note shape is therefore a practical necessity, as it allows for note-to-note relationships to be immediately understood, as well as for larger rhythmic patterns to be readily grasped. Western rhythmic notation since 1600 contains a large (and desirable) degree of redundancy, as note shapes, note spacing, layout, bar-lines and time signatures all facilitate the apprehension and performance of rhythmic patterns.

We are most familiar with representations of duration in terms of strict ratios such as 2:1, 3:1 and in some musics 3:2. Indeed, the history of Western rhythmic notation has to do in large part with the changing ways in which such durational proportions might be represented. It cannot be overemphasized, however, that the notational representations of these rhythmic relationships are not congruent with the durations as they are performed or perceived. A large and growing body of data on performance timing demonstrates that human performers never produce such ratios when they play, though they do produce highly nuanced timings in a consistent manner (see §III, 5). Nor do listeners expect such ratios in performance (see Repp, I1995–6). It is thus an open question, although increasingly doubtful, whether these arithmetically regular ratios represent the ‘underlying structure’ of durational relationships (even though they are present only in the case of electronic or mechanical performance), or whether the irregular ratios (which are consistently reproduced in performance) represent the ‘real’ structure and the notated proportions are simply a convenient shorthand.
A notational system that employs a 1:2:3 set of proportional signifiers is capable of rendering a very complex set of relative durations by the concatenation of durational values through ties (or other ligatures, such as dots of addition), as well as through the nesting of concurrent durations. While rhythmic relationships involving other prime numbers (e.g. 5:3, 7:2) are logically possible, these do not appear as basic orthographic relationships in either Western or non-Western notational systems, even though such ratios may be a truer representation of durational relationships as they are performed. Instead, the same proportional signifiers tend to be used in a broad variety of actual practices. For example, the characteristic execution of the ‘same’ minim–crotchet figure in Viennese waltzes and ländler is quite different, and thus one could conceivably use different orthographic representations to indicate their respective durational nuances. Rather, we assume that the performer knows how to execute the rhythmic figures in the appropriate manner characteristic of a given genre, and/or we use various expressive descriptions (con anima, dolce, langsam etc.) which systematically vary the timing of the durations relative to their ‘deadpan’ values. The use of a few lower-order prime values in systems of rhythmic notation, supplemented by expressive terms or generic performance conventions, supports the hypothesis that successive durations are produced and perceived in terms of a limited number of cognitive categories. As a result, only a few basic durational values are required by any notational system.
The notations given in ex.15 are alike in one important respect in that they give no direct indication of tempo. Once the proportional relationship among successive durations has been established, the tempo may be indicated either by defining an integer unit of duration (which then defines other values in relation to it) or by giving a general indication of the sense of movement the passage is supposed to exemplify. Since the advent of the metronome, tempos have been indicated by correlating some durational unit (usually a crotchet) with a unit of clock time (expressed as beats per minute). The choice of an integer unit of tempo or tactus acts as a constraint on rhythmic notation, as it is sensible to keep the beat unit in the middle of the range of durational values. If relatively short values are used to indicate faster tempos, then still shorter durations will be required to indicate subdivisions. Conversely, if long values are used to indicate slower tempos, then even longer durations will be needed to indicate measure spans and other composite durations. While the use of long versus short durations (and, concomitantly, large versus small metres, such as 4/2 versus 4/8) to indicate different tempos has a long history, such usages skew the distribution of durational options on the composer's notational palette. It was therefore inevitable that as the integer unit of time shifted from the breve to the semibreve and then to minim over the 13th, 14th and 15th centuries, even shorter durational values (semiminimae and fusae) appeared at the same time (see Sachs, A1953).
Notational systems (and theories of rhythm) reflect not only contemporaneous musical practice but also the temporal sensibilities of their day. For example, Berger (B1993) has remarked that 14th-century rhythmic notation draws on the system of Roman fractions then in use, while the use of proportional signs in Renaissance music reflects the shift to Arabic numerals and the rise of commercial arithmetic. Indeed, without an understanding of contemporaneous concepts of time and counting, understanding a system of rhythmic notation or discussing it theoretically may be all but impossible.
Rhythm, §II: Historical studies of rhythm
The history of the relationship between words and music is characterized by a tension between accommodation and domination. This tension is chiefly felt in the domain of rhythm. One should first note that music and speech are both made up of a time-dependent sequence of elements, in which pitch, duration and dynamics play a critical part. Language and music are similarly constrained by the limits of our ears, mind and memory. That there are structural parallels between the two is therefore not surprising. For example, Handel (I1989) notes that linguistic stresses and musical metre (and metric accents) operate under similar timing constraints, and Lerdahl and Jackendoff (E1983) argue that there are important parallels between the hierarchic structures of musical rhythm and prosodic timing in language. Yet there are also important differences. First and foremost is that speech is made up of phonological segments that have their own intrinsic durations and durational relationships, whereas music is made up of rhythms which have no absolute value. Speech consists of phonological segments and phrases separated by pauses of variable length. Normal speech is also only ‘locally rhythmic,’ in that it is only within the context of a breath group or subgroup that one finds patterns of stress or accent. By contrast, in music one normally fits successive motifs and phrases into a common, continuous metric framework. Many of the phonological elements of speech are extremely brief, such that timing differences of as little as 10ms can mark the difference between phonemes. Vowel sounds are much longer, and their timing more variable (though such variation is in general quite systematic, such that a given vowel in a given phonological and semantic context usually has determinate duration). Musical durations are even longer, 100ms being a typical threshold of sensitivity and 200ms a minimally significant duration (see Butler, I1992). When set to metred music, the normal rhythms of speech are seriously distorted, mainly by lengthening vowels but also by fitting the segmental pauses of speech within the constraints of the musical metre.
In Western culture the tension between words and music goes back to discussions of rhythmics and metrics by the ancient Greeks (see Mathiesen, B1985). Written poetry, of course, requires no exterior (i.e. musical) notation in order to mark its rhythmic organization and structure, as the layout of the poetic text into lines and stanzas is usually sufficient to make its rhythms clear. Agawu (J1987) notes that, rather than positing a simple dichotomy of poetry and prose, one can distinguish between normal speech, declamatory speech (in which the rhythms are exaggerated but still grounded in normal speech) and metred speech (in which normative rhythms and phrase structures of language are subject to occasional distortions, enjambment and so forth). Even in metred speech, however, the rhythmic structure can be said to be linguistic rather than musical in origin, as the placement of syllables and syntax is not arbitrary but governed by the stress and timing rules of the language. Moving beyond metred speech to musically metred contexts, the morphophonemic aspects of the text may still have influence. Palmer and Kelly (I1992) show that the compound word rule and the nuclear stress rule – two cornerstones of English phonological structure – tend to coincide with musical rules of metrical accent in both composition (i.e. metric and rhythmic structure of a melody relative to the text underlay) and performance (i.e. the use of expressive agogic or dynamic accent). Thus the relation between speech rhythm and musical rhythm is not a simple opposition, but a complex and multivalent interchange.
Musical notation may not always clearly and accurately reflect the relationship between text and music, the evolution of the notation for recitative being a case in point. In the first decades of the 17th century Italian composers such as Peri, Caccini, Agazzari, Gagliano and Monteverdi who wished to indicate passages in stile rappresentativo wrote out musical approximations of the natural speech rhythms in a manner analogous to French settings of vers mesurés. Yet the representation of speech rhythms by a limited number and proportionally specific set of durational values hardly yielded accurate or natural results. Thus by the century's end this practice had been abandoned and most recitative was notated in rapid and even notes (crotchets or quavers), with the understanding that the rhythm would follow that of the speech declamation. Grounding the rhythms of recitative in speech also means that the singer need not worry about precise coordination of most syllables with the accompaniment, save at cadence points.
Over the course of Western music history shifting cycles of musical versus textual domination can be observed. The modal rhythm of Notre Dame polyphony was rooted in the predominantly iambic accentual declamation of its Latin poetic texts (see Gillingham, B1986). Yet modal rhythm opened the door to a written tradition of music where rhythm could be a wholly independent compositional element, and once such independence was possible it became a resource to be explored (and exploited) in its own right. Indeed, with the rise of the motet style in the 14th century the expression of the ‘natural’ rhythms of the poetic texts had been all but abandoned in composition of increasingly complex polyrhythmic textures. This excessively ornate rhythmic practice gave way to the rhythmically simpler textures of the 15th century, culminating in Josquin's crystalline settings of texts which, while thoroughly musical in conception, nonetheless complement and accommodate the accentual structure of the language. At the end of the 16th century and the beginning of the 17th the experiments with vers mesurés in France and the rise of monody in Italy were indicative of yet another attempt to restore rhythmic priority to the text. The new practices of text-setting did not involve only a rejection of textural complexities, since a homorhythmic disposition of the text in the 16th-century madrigal and chanson was already common. Rather, and once again, the battle between text and melody concerned their rhythmic particulars, not their tonal contours.
See also Metre.
Rhythm, §II: Historical studies of rhythm
As Crocker (B1990) notes, while specifying durations entails the coordination of voices, specifying the coordination of voices need not entail precise specification of durations or proportions. Coordination must therefore be understood in its broadest sense – ensuring that various sections and pieces as a whole begin and end together – without necessarily requiring moment-to-moment coordination among individual parts. Not surprisingly, in early polyphony this first involved coordination of the added part(s) relative to the tenor, which in turn guaranteed a rough degree of coordination among the added parts themselves.
In polyphonic music before the invention of modal rhythm the question arises as to whether in performance one will have isochronous notes or isochronous syllables. This is roughly analogous to having regular beats but flexible subdivision (yielding evenly spaced syllables), as opposed to regular subdivision (yielding evenly spaced notes) but irregularly spaced syllables – in short, divisive versus additive approaches to musical time. In either case, the rhythmic breakthrough that occurred in Notre Dame polyphony marked the clear emergence of at least one level of isochronous time which then could serve as a scaffold for the others. Moreover, this temporal scaffold was neither ‘in the music’ nor ‘in the words’. It had a life of its own as a pre-compositional framework, which might or might not be audible in performance. Modal rhythm and its subsequent revisions opened manifold possibilities for temporal coordination, as it became possible to conceive of temporal coordination against an abstract series of perfections rather than in terms of one actual part against another. One could also treat a series of such units as a larger span whose rhythmic contents can be determined by subsequent division and calculation, as in the case of isorhythmic forms. As the framework for temporal coordination grows larger (e.g. in cases of isorhythm) it usually cannot be understood ‘in time’ – that is, in performance – but can only be discerned ‘out of time’ when one has a global view of the musical whole. Such a perspective on musical rhythm is reminiscent of Boethian notions of divine time and temporality, in which the composer has complete possession, all at once, of the life of the composition.
The earliest Western polyphony was notated in score format, which gave an immediate sense of synchronization of its component voices. The shift from score notation to partbook or column notation (with the tenor at the bottom) presupposes the presence of an abstract series of durations which governs the rhythmic structure in each part. While in some instances this may have been the tenor part itself, as the rhythmic complexity of the tenor increased some abstract temporal measure would seem to be obligatory. Indeed, as the proportional relationships grew more arcane the absence of a score may have been more of a help than a hindrance to the performer. As can be seen in ex.16, when all parts of Amans, ames secretement are laid out in score, the result is dizzying.

In the music of the common practice period the coordination of various parts relative to an externalized metre became such a deeply rooted aspect of Western musical culture that its presence has gone largely unnoticed. It is perhaps for that reason that the graphic notation used in works by composers such as Boulez and Cage still strikes us as revolutionary, for not only do such scores lack pitch and durational specification among their parts, they also have loosened or even abandoned any pretence of coordination among them. Interestingly, many pieces in graphic notation, such as Berio's Sequenza III (fig.1), make use of stopwatch timings to determine structural articulations. As with the music of the Middle Ages, this mode of temporal reckoning is not intrinsic to the temporal activity of any part of the music itself, but must be imposed from without.
Coordination of parts is an issue on smaller as well as larger levels. In the performance of polyrhythms (duple or quadruple in one part versus triple in another) the question arises as to whether individual parts are to be performed as notated, or whether in some cases one rhythm should be ‘assimilated’ into another. In ex. 17, should the parts on the bottom staves be even duplets, or should they be realized as long–short figures in coordination with the treble triplets? Neumann (A1987) argues that bona fide cases of polyrhythms did occur in 16th- and 17th-century musical practice, but he also proposes that under certain conditions assimilation ought to occur. Eibner (H1962) addresses similar issues in the music of Schubert. The ‘assimilation question’ presupposes two important points: that in cases of assimilation a particular metric framework is operative (and indeed that one framework is dominant), and that under certain conditions the rhythmic proportions as notated are not to be taken at face value.

Rhythm, §II: Historical studies of rhythm
Around 1600 a dramatic change took place in Western rhythmic notation: a shift from mensural practices which had been in place since the 14th century to modern, orthochronic notation in which the proportional relationship between any two symbols in the notational system remains constant. As Rastall (A1982) observes, this was not accomplished all at once, and indeed rests had been orthochronic since the end of the 13th century. The emergence of modern rhythmic and metric notation involved more than the streamlining of proportional possibilities down to the binary logic now in use. Concomitant with the adoption of binary relationships for normative durations (itself a historically contingent reflection of the predominant rhythmic practices of the day) one also finds the use of bar-lines, ties and tempo terms. Many of these features appeared before 1600: bar-lines can be found in Ars Nova keyboard scores and in keyboard and lute tablatures; ties appear in Cavazzoni's print of 1523 (again, of keyboard scores), and tempo terms can be found as far back as the St Gallen manuscripts. Yet the appearance of this constellation of notational features at approximately the same time is significant, for it indicates that a basic change in the rhythmic foundations of Western music was under way.
The phrase ‘modern metre’ denotes metre as defined in §I, 4: the presence of a hierarchic pattern of beats that are felt by both performer and listener, even if they are not articulated directly by the durations in the music. On this view, the history of metre in music is wonderfully heterogeneous. Before 1600 some music was metric, while other music was not; after 1600 most music was metric, though there were exceptions (e.g. unaccompanied recitative and the unmetred keyboard preludes of Louis Couperin and d'Anglebert). Moreover, Western notation as it evolved from the 12th century to the 17th was equivocal regarding metre, and so one must look not only at the notational system but also at its implementation in particular contexts and genres.
The quatre prolacions of Philippe de Vitry and their Italian analogues of Marchetto da Padova are strikingly similar to the duple versus triple metres with simple versus triple subdivisions of modern usage. Yet there are important differences. First, in the Italian system different degrees of subdivision give rise to different mensurations (e.g. quarternaria versus octonaria and senaria perfecta versus duodenaria perfecta). While we would consider these to be different varieties of simple duple and simple triple metre respectively, in the Italian system they are regarded as different metres. More important is the question whether these prolacions represent true metre signatures or are more like durational signatures (see Berger, B1993). While medieval and Renaissance systems of notation provided a means of expressing complex durational relationships within and among the various parts, as in ex.16, such usage is no more metric than much 20th-century music ostensibly written in a particular metre (fig.2). In neither case can the presence of metric notation be equated with the presence of a metre. We may contrast these arithmetically clever uses of mensural notation with that found in the formes fixes of the same era – music with a far greater degree (or at least potential degree) of metricity. Typical practice involves a single mensuration in all voices, and often changes of prolation are used to mark different sections of the work, as in ex.18. Indeed, the presence of such metric shifts presupposes a metre that is to be shifted.

If the notational system of pre-tonal music is equivocal with respect to metre, other rhythmic features are nonetheless indicative of the degree of ‘metricity’ of a particular piece or genre. One such feature is the presence or absence of anacruses. As Sachs observed:
We might look over hundreds and hundreds of polyphonic pieces from the Middle Ages and the Renaissance and never find an upbeat. … An actual upbeat – like winding up for a throw – prepares a stress; it is necessarily four-ONE. It was out of place in the polyphonic forms which depended, on the whole, upon an even, little-stressed flow. (A1953, p.261)
While bar-lines are an obvious way of marking an upbeat figure, the presence of initial rests also indicates a sense of arsis and thesis which underlies a true metre. For if there is no motional difference between beats, then there is no sense of metre, in which case no real anacrustic gestures are possible. Syncopations, or more precisely syncopations felt as suppressed beats, are also indicative of metre.
Various topics in theoretical sources from the 17th century and the early 18th indicate a concern with metre and its relation to the rhythms of music and text, and in purely instrumental performance. Butler's commentary cited above (§I, 1) on the subjective differences between running subdivision in compound duple versus simple triple time signatures presupposed the kind of metric listening that would make such differences manifest. Subsequent theorists, such as Diruta (C1593–1609), Printz (C1689) and Heinichen (C1728), discussed the subjective nature of metre under the rubric of quantitas intrinsica. Walther's Lexicon of 1732 gave the following definition:
Quantitas notarum extrinsica, and intrinsica [Lat.] is the apparent (or outward) and the inner value of the notes. According to the former, every note is performed equal to other notes of the same value, but according to the latter the notes are of unequal length: since, to be specific, the uneven-numbered parts of the beat are long and the even-numbered ones short. (cited in Houle, A1987, p.82)
Houle gives a thorough discussion of quantitas intrinsica and the ways in which the distinctions between ‘good’ and ‘bad’ beats were made manifest in performing practice via notes inégales, keyboard fingerings, tonguing and bowing conventions. Houle also gives a survey of discussions on rhythmopoeia, or verse metrics, as they were applied in various metric contexts. He notes that ‘the chief problem in theories of rhythmopoeia was the relationship of measures, with their time signatures and regular barlines, to the various and changing phrases made up of musical feet’ (p.77) – that is, whether these rhythmic archetypes existed prior to metre or vice versa. The historical significance of such a question is that it could not even be formulated if the music of the Baroque and early Classical eras lacked metre in the modern sense.
Broadly speaking, the depth of metric organization seems to have increased since the Renaissance era. In ex.19a motoric rhythms are manifest in terms of a continuous pulse and a constant two-beat pattern, but no higher levels of metre emerge (see Botelho, E1993). In ex.19b one finds regularities of both metre and phrase on the two-bar and even four-bar levels. Indeed one finds such regularities in simple dance music from medieval ductiae and estampies to disco of the 1970s. It was in the Classical style that the periodic phrasing of dance music became pervasive in other genres, and so we find regular layers of metric organization above the notated bar. While musical forms grew more expansive in the 19th century, by and large metric structures did not; this may be a contingent aspect of the style, or a reflection of deeper syntactic and/or psychological constraints on metric structure. Ex.21c is a re-notation of Bruckner's Fourth Symphony (after Lester, E1986). Here each duration is one quarter of its original value, which allows one to see how each group of four bars functions like a beat in a measure, and these hypermeasures themselves are rhythmically paired and quadrupled. Bruckner's music contains rhythmic patterns and measures that are indeed of a ‘higher order’.

Rhythm, §II: Historical studies of rhythm
As rhythm is not just a sense of durational organization, but also (and perhaps foremost) a sense of coordinated movement, a chief concern in understanding and performing musical rhythm involves the determination of tempo. The presence of a continuous series of brief durations need not entail a sense of rapid tempo, just as a series of longer durations need not entail a sense of slower motion. Nor does the subdivision of a duration into notes a half, third or even quarter of the original value necessarily give rise to a doubling, trebling or quadrupling of the perceived motion. Thus the first issue to be sorted out in discussions of tempo is whether a marking, descriptive term or theoretical discussion refers to particular durations (either phenomenally present in the music or in a more abstract, counted beat) or to the overall impression of motion. A metronome marking of crotchet = 120 and the Italian directive allegro non troppo may give rise to the same musical effect, but they are fundamentally different modes of description. As Epstein notes, tempo
is a consequence of the sum of all factors within a piece – the overall sense of a work's themes, rhythms, articulations, ‘breathing’, motion, harmonic progressions, tonal movement, contrapuntal activity. Yet tempo … is a reduction of this complex Gestalt into the element of speed per se, a speed that allows the overall, integrated bundle of musical elements to flow with a rightful sense. (H1995, p.99)
A sense of tempo and motion is a hierarchically emergent property of the musical surface, and not simply a product of note-to-note transitions.
Given that tempo is a composite effect of the musical structure, and given the ways various parameters may interact in performance, tempo – or more precisely understanding and achieving the right tempo – will always be an elusive target, even in musical styles that are familiar and whose performing practices are well documented. ‘Correct’ tempos for any work or genre may cover a fairly wide range. Indeed, one of the principal ways a performer may distinguish his or her interpretation of a work is through choice of tempo. For earlier musics, a certain degree of historical opacity with respect to previous tempos is inevitable; as Planchart notes:
Actual tempo will always remain an educated guess at best. Any attempt to provide dogmatically exact tempos for any music written before 1600 is neither historically accurate nor ultimately satisfactory scholarship. To this extent, then, each performance is a mixture of hypothesis, special pleading, and an Augustinian leap of faith. (C1975, p.156)
Planchart's caveat can reasonably be extended to all musical styles, both before and after the rise of modern rhythmic notation.
Any temporal process may function as a clock or time-keeper if we believe that it is a reliable and accurate counter against which other, less regular processes and events may be measured. Since musical time inevitably involves the ebb and flow of longer and shorter durations, musicians have often sought extra-musical sources as a reference for musical durations and tempo. Thus heartbeat rate (from Ramos de Pareia, C1482, to Quantz, C1752), breathing rate (Gaffurius, C1496) and walking period (Buchner, Cc1520) were used as temporal benchmarks. These descriptions of physiologically or physiognomically based tactus presage the discussions of natural pace and spontaneous tempo in modern psychology, which, while tending to discount the effect of heart and respiration rates, reaffirm the kinaesthetic aspect of tempo giusto and add a neurobiological component. From the Baroque period physiology was replaced by physics, from the use of pendulums as proposed by Mersenne (MersenneHU), Thiémé (D1801) and Mason (D1806) to the mechanical escapement metronome made famous by Maelzel (1815, actually stolen from Winkel; see Epstein, H1995).
Whether biological or mechanical, these sources of extra-musical periodicity could be used to establish the duration of a musical or motor behaviour, which in turn could define the durational values given in notation. From the Renaissance this fundamental period was known as the Tactus, corresponding to what we call either the measure or the beat. While the terms ‘tactus’, ‘beat’ and ‘tempo’ are often used interchangeably, historically they have designated different aspects of musical time and time-keeping. Tactus refers to the keeping of time by beating with the hand, first described by Adam von Fulda (C1490). At its simplest ‘the mensural system related to notes to a down-and-up gesture of moderate speed called the tactus’ (Bank, A1972; Houle, A1987). As Sachs notes, ‘the tactus was wholly unconcerned with the actual rhythm, with grouping or accent. It just maintained the even pulsation of units, and nothing else’ (A1953, p.242). In this context, the tactus remains constant, and all tempo differences are expressed by the use of proportion and mensuration. Indeed, this becomes the raison d'être for the various proportions and their elaborate theoretical discussions: in order to express a moderately faster tempo one uses a particular proportion (e.g. 3:4 or 2:3) relative to the background tactus. The principal problem, given this assumption, is to determine which notational symbol corresponds to the tactus.
A number of factors complicate this approach to tactus. While at some times the tactus may have typically corresponded to a particular durational unit, at other times it may have corresponded to a multiplicity of note values. This implies that the choice of a beat-unit of notation was arbitrary. Yet time signatures do carry associations of tempo: 3/2 is slow, 3/4 is moderate, 3/8 is quick. Under these different metres the tactus inheres at the minim, crotchet and quaver respectively. Moreover, the tempo relationships are not twice as fast (3/4 to 3/2) and twice as fast again (3/8 to 3/4), but span a narrower range (see Rastall, A1982, pp.188–91). Complaints about the vagueness or unreliability of characterizations such as C as ‘little faster than C’ and as ‘quickest of all’ fail to note that the descriptions of categorically different tempos (each of which spans a range of acceptable values) are inherently fuzzy. Such descriptions are also indicative of another complication: that the tactus was not constant but varied, and indeed that the different varieties of mensuration are indicative of the presence of a faster or slower tactus. Discussions of variable tactus may still make reference to heartbeat and respiration rate, but rather than using such physiological processes to specify the tactus, they are instead used to establish a moderate beat, from which faster or slower tempos can be determined.
A further complication is that there are several ways of beating the tactus. In both duple and triple time the tactus consisted of an upbeat and a downbeat, with the distinction that in triple time the downstroke was twice as long as the upstroke; these were referred to as equal and unequal tactus respectively. In the triple tactus what we would consider the second beat of the measure is unmarked; this practice is analogous to the ‘empty’ (i.e. non-articulated) beats in the counting of tāla in Indian music. Given that both duple and triple tactus occupy the same span of time from downstroke to downstroke, this means that the beats within duple and triple patterns move at different rates. Moreover, the duple tactus could be performed normally (tactus major) or twice as fast (tactus minor). Ornithoparchus (cited in Houle, A1987, p.4) remarked that tactus minor ‘is allowed onely by the Unlearned’, which implies that tactus minor was in fact the counting of subdivision, as would typically be involved in the instruction of a novice performer. Given that during the late 16th century and the 17th subdivision was almost exclusively duple, the absence of theoretical discussions of an unequal tactus minor (i.e. a beating of triple subdivision) is understandable. Yet this raises yet another question: whether the tactus pattern corresponds to the downbeat or to the individual beats within the measure, since a slow tactus minor could indicate entire measures in rapid tempo, for example. Ultimately, one must look to the particular piece of music and use a performer's common sense. Just as the crisp execution of a complex rhythmic unison may require a conductor's use of rapid subdivision, so too may the coordination of several rhythmically dissonant parts require the use of larger time units to mark points of coincidence among them.
Just when the connections between tactus and mensuration became most confusing, one begins to find the widespread use of tempo terms like ‘adagio’ and ‘presto’. The increased use of tempo terms accompanied the rise of instrumental music, since in the absence of a text or liturgical context (which would, one assumes, give a sense of the mood and suitable tempo for the music) descriptions of expressive mood, including tempo, were of practical use. The earliest signs of such usage can be found in the tablatures of the vihuelists (starting with Milán in 1536), who used the terms despacio and apriesa. Tempo and expression markings appear in Italian musical sources around 1600 (e.g. Gabrieli, 1597; Caccini, 1601; and Frescobaldi, 1615). There is also what one might call a ‘syntactic’ reason for the common usage of tempo terms around the turn of the 17th century. With the shift to orthochronic notation, the durational relationships among various notes no longer had to be indicated by a mensural sign, and the layout of a score, particularly through beams and bar-lines, was sufficient to make the hierarchic relationships among the various rhythmic levels immediately apparent. What the orthography could not do was to indicate which level of the rhythmic hierarchy was to function as the beat. As noted above, the emergence of modern metre involved the enrichment of the metric hierarchy by the addition of levels of regularity below and (especially) above the beat. This being the case, even if orthography makes those levels distinct, the problem now arises as to how the various levels of rhythmic duration correspond to the different levels of the metric hierarchy. Time signatures and tempo terms work in tandem to specify the beat level and indicate a sense of pacing for both that level and the rhythm as a whole. The hierarchic nature of metre, and the challenges it presents regarding the determination of tempo, may also explain why the relationship between time signatures and tempo received so much attention from 17th- and 18th-century musicians and theorists.
A common complaint in the 1960s and 70s was the relative impoverishment of rhythmic theory and analysis. Since then there has been a great flowering of research in rhythmic theory, analysis, perception and performance. The following discussion serves as an introduction to those research areas that have received the most attention in recent decades. While research on musical form, tonality, styles, composers and particular compositions often touches on rhythmic issues, this survey is restricted to those theorists, musicologists, composers and psychologists whose work centrally addresses questions of rhythm, metre and musical time.
See also Analysis; Atonality; Form; Philosophy of music; Proportional notation; Psychology of music, §§I, II, 2; Serialism and Set.
1. The hierarchic depth of rhythm and metre.
3. Lerdahl and jackendoff's ‘Generative Theory of Tonal Music’.
4. Post-tonal rhythm and metre.
5. Psychological studies of rhythm and metre.
6. Musical time and temporality.
Rhythm, §III: Current rhythm research
Various authors have maintained that rhythm and form are one and the same, and that the different words are simply commonplace terms to describe the same processes on different structural levels. Cone, for example, claims that ‘certain general principles underlie common formal units … and that the same principles, working on higher levels and more comprehensive formal sections, can ultimately be invoked to explain an entire composition as one all-embracing rhythmic impulse’ (E1968, p.39). These principles may be quite concrete, as in Cooper and Meyer's (E1960) attempt to extend their basic archetypes for note-to-note patterning to the highest levels of rhythmic form, so that, for example, the first movement of Beethoven's Eighth Symphony could be regarded as one giant anapaest (Meyer subsequently recanted this position; see Meyer, E1991). They may also be more abstract; for example, Berry posited that musical structures large and small involve ‘the punctuated shaping of time and space into lines of growth, decline, and stasis, hierarchically ordered’ (G1976, p.5).
The investigation of proportional relationships is another way in which a principle of foreground rhythmic relationships, namely the relative duration of successive notes, is applied to larger musical units, including complete works. Various composers, from Machaut to Bartók, have used proportional relationships as part of their compositional technique (see Numbers and music), and this compositional usage of proportion has been documented by various scholars (e.g. Howat, F1983, on Debussy; Lendvai, K1955, on Bartók; and Kramer, K1988). Other studies (e.g. Rogers, K1977; Perry-Camp, K1979; and Smyth, E1990) seek to find significant proportional relationships in other music (i.e. Mozart and Chopin) where it was not part of the composer's conscious compositional method. Of special interest in these studies are ‘golden section’ relationships (1:1·618) (see Golden number) such as those based on the Fibonacci series (1, 2, 3, 5, 8, 13 …).
On the other hand, the terms ‘rhythm’ and ‘form’ may be used precisely because there are fundamental differences between the arrangement of notes and small note groups into motifs and phrases, and the arrangement of larger units into complete movements and pieces. It is not the fact that music is hierarchic which blurs the distinction between rhythm and form; rather, it is the degree to which one regards the musical hierarchy as recursively organized that leads to a blending of rhythm and form. A recursive hierarchy is one in which a single principle (or set of principles) controls the structure from top to bottom (or bottom to top). Arguing against recursion, Meyer notes that ‘the way in which a particular parameter acts in articulating structure may be different on different levels’ (E1973, p.89), and Brower (E1993) proposes a threefold division of rhythmic and musical structure as a reflection of different perceptual and cognitive processes.
Just as one may examine the limits of rhythmic structure, one may also examine the limits of metric, or more precisely hypermetric, structure. While few would deny that the metric hierarchy may extend above the level of the downbeat, there are a variety of theoretical positions with respect to the possible depth of hypermetre and the particulars of hypermetric (as opposed to simple foreground metric) syntax. While some theoretical positions may be characterized as more or less sceptical with respect to hypermetre, the question of how ‘hyper’ hypermetre can be is actually a constellation of questions. First, is hypermetre commonplace or relatively rare? Lester (E1986) discusses the metric and hypermetric structure of Bruckner's Fourth Symphony (see ex.19d) and notes that this kind of large-scale metre is quite exceptional in comparison with other supposed cases of hypermetre (i.e. in the context of normative four-bar phrases). If a hypermetre is present, is it as robust as foreground metre? Cohn (G1992–3), in discussing the Scherzo of Beethoven's Ninth Symphony, notes how hypermetric analyses must often deal with conflicting sources of metric accent and organization that do not arise in determinations of foreground metre. Do hypermetres follow the same syntactic constraints as does metre in the foreground (i.e. do hypermetric units need to be isochronous)? Kramer (K1988) claims that hypermetric regularity can be based on the presence of an equal number of elements (hyperbeats) within each hypermeasure, even if those beats are not isochronously spaced. Does hypermetre extend to the deepest levels of structure? Kramer (K1988) and Komar (E1971) give hypermetric analyses that span entire movements, while Lerdahl and Jackendoff (E1983), Benjamin (G1984) and Lester (E1986) caution that metre is primarily a feature of the foreground. Rothstein (E1989) discusses the interaction between hypermetre and phrase structure and the extent to which their interaction obeys the same constraints as metre and grouping in the foreground.
Non-Western musics are sometimes said to exemplify the inherence of rhythmic and metric structures on higher levels of structure. For example, some 14- and 16-beat tāla in Indian music, which in slow tempos can last some 30–40 seconds, might be regarded as a class of hypermetre. In the case of Indian music, different levels within the cycle are recognized as comprising different elements – āvarta for the entire cycle, vibhaga for subsections (of varying length) and mātrā for the smallest counting units. Similarly, in the classical music of central Java rhythmic cycles may comprise as many as 128 or 256 beats, with subcycles marked by various colotomic divisions. In the gamelan there are certain instruments whose sole function is to mark off the larger temporal units. Most notable are those instruments whose function lies in marking the largest cycles, including the kenong, which marks intermediate cycles, and the gong ageng, which marks the largest cycle. Other instruments, such as the saron, repeat the basic melodic skeleton. Some caution in describing these tāla and gong patterns as species of metre is in order, however. While the terms for various tāla and colotomic patterns span a large range of temporal structures (which implies a fusion of rhythm and form), one should understand the social conditions of their usage. In Indian music there is a rich theory and practice of categorizing and performing rhythmic patterns (‘counting tāla’), and so it makes sense that larger units may be described by adapting or analogizing a standard nomenclature. Similarly, in Javanese music, given the special religious and social significance of the gong ageng in the gamelan it is logical that musical form and organization are described relative to its activity. To consider an analogous case from a Western musical context, one could regard a 16-bar Classical minuet (which would be played continuously for a social dance) as a cycle of 96 beats when played with repeats. Indeed, in terms of the minuet-as-danced the global repeat of the form would represent a kind of āvarta (literally, ‘turning back’). Perhaps if classical chamber orchestras contained instruments like the gong ageng a minuet might well be described as a large cycle of beats (or steps). The fact that it is not reflects both the different conditions under which Western music is produced and the fact that, in describing the organization of common practice music, Western musicians and theorists were able to co-opt terms from language and rhetoric (e.g. ‘clause’, 'sentence’, ‘period’) and thus did not have to extend rhythmic and metric terminology beyond the musical foreground.
Rhythm, §III: Current rhythm research
Rhythmic issues have received considerable attention from Schenkerian theorists and analysts in recent decades. While Schenker himself made clear ontological distinctions between background levels and the middleground, and between middleground and foreground, it is in distinguishing between middleground levels that Schenker's original work is most under-theorized (Cadwallader, E1990). In examining how tonal and rhythmic processes interact to define various middleground structures, the study of rhythm may be seen as an essential continuation of the Schenkerian theoretical project.
For most Schenkerian theorists pitch relationships remain analytically prior to duration and rhythm: ‘all rhythmic patterns of middleground levels are determined exclusively by pitch criteria’ (Yeston, E1976, p.84). This priority of pitch explains why the basic level of rhythmic analysis in Schenkerian contexts is usually the phrase, since the phrase is the smallest level where one may find a complete linear motion. Thus, for example, investigations into the nature of rhythmic accent typically begin with a consideration of accent on the phrase level, whether or not phrase beginnings (or endings) have metric or rhythmic accents, and so forth (see Kramer, K1988). While Cone (E1968) treated rhythm (among other topics) from a perspective informed by Schenkerian theory, the first important work to focus on rhythmic and metric issues from a Schenkerian standpoint was Komar (E1971). His discussions of metre, hypermetre, metric displacement and rhythmic reduction presaged the work of many subsequent theorists. However, Schachter's three articles in The Music Forum (E1976, E1980, G1987) remain the locus classicus for Schenkerian studies of rhythm. As Krebs notes, ‘Schachter has two basic aims in his articles. First, he sets out to vindicate Schenker from allegations of having neglected rhythm’ and then uses ‘Schenker's cryptic though evocative remarks on rhythm as a springboard for his own ideas’ (G1992, p.82). Schachter draws many parallels and analogies between surface rhythm and metre, so that extended anacruses, rhythmic motifs and metre itself may be writ large in the middleground. Schachter also develops the technique of ‘durational reduction’ as a rhythmic analogue to pitch reduction, whereby middleground pitches are given specific durations which relate to the foreground durations by some constant factor (ex.20). While this is not new, Schachter was the first to apply durational reduction to extensive portions of the middleground. Schachter differentiates between tonal rhythm and durational rhythm, the former stemming from the rhythmic properties of the tonal system itself, the latter from patterns of emphasis, duration and grouping which do not arise from the tonal grammar. Rothstein (E1981, E1989) gives greater rigour to Schachter's ideas of durational reduction, drawing equally on the work of Koch and Schenker. He proposes a normative archetype for phrase rhythm (itself a combination of tonal and durational rhythm) and then discusses some of the ways in which normative middleground archetypes may be transformed into less regular foreground structures.

Another aspect of rhythmic theory and analysis which has received attention from theorists who espouse a Schenkerian perspective involves discussions of rhythmic or metric ‘dissonance’ (Yeston, E1976; but see also Stockhausen, F1963). Such dissonances occur when there are two rhythmic levels or strata such that one cannot be expressed as a simple multiple of the other – in other words, a polyrhythm such as two against three (hemiola) or three against four. The result is a non-congruence of durational and/or accentual patterns between the two strata. This non-congruence may be local, as in an isolated hemiola, or it may extend over a larger period of time. Krebs (G1987) points out that if two rhythmic strata are offset they may also create a dissonance, even if one is a multiple of the other. Further refinements to the taxonomy of metric consonance and dissonance can be found in Cohn (G1992; G1992–3) and Grave (G1995). Metric dissonance in its most robust form involves the presence of two (or more) metres, as described by Schachter (G1987), Rothstein (E1989, G1995) and Kamien (G1993). In a somewhat less robust form one may speak of latent metric dissonances, what Willner (G1996, E1998) terms ‘counterstress’ and Samarotto (E1999) ‘shadow metre’.
See also Analysis, §II, 4, and Schenker, Heinrich.
Rhythm, §III: Current rhythm research
The publication of Lerdahl and Jackendoff's Generative Theory of Tonal Music in 1983 was both a response to previous work in rhythm and tonal structure and a ground-breaking volume which brought evidence and insights from linguistics and perceptual psychology to bear on problems of musical rhythm, tonality and form. The book has spawned a great deal of research in perception and cognition, as it makes claims that can be empirically tested (e.g. Deliège, I1986–7; Palmer and Krumhansl, H1987; and Bigand, I1990). It has also generated numerous responses in both psychology (Rosner, I1988; Clarke and Krumhansl, I1989–90) and music theory (Peel and Slawson, E1984; Hantz, E1985; and London, E1997).
Lerdahl and Jackendoff's psychological approach to questions of rhythm and tonal structure is apparent from the first sentence of the book: ‘We take the goal of a theory of music to be a formal description of the musical intuitions of a listener who is experienced in a musical idiom’. Hence an understanding of the physiological and psychological process by which musical patterns are perceived, remembered and understood is essential to the authors' research project. From this perspective Lerdahl and Jackendoff can give a psychological rationale for reductive models of musical structure (and in particular Schenkerian models, on which their theory relies). This is stated in their ‘Reductive Hypothesis’: ‘The listener attempts to organize all the pitch events of a piece into a single coherent structure, such that they are all heard in a hierarchy of relative importance’. The book's premise is that without such a reductive process the listener cannot manage the vast amount of sonic and musical information presented in a piece of even modest dimensions. Along with psychology, A Generative Theory of Tonal Music also draws on work in linguistic prosody to bolster and complement claims regarding the manner in which musical rhythm is structured, implying that some aspects of music and language may share common cognitive domain(s). The book also takes from linguistics the notion of a transformational grammar, so that certain structures (such as phrase overlaps) are accounted for in terms of a base structure that underlies more complex rhythmic phenomena on the musical surface. Lerdahl and Jackendoff distinguish between obligatory and optional structures by differentiating between ‘well-formedness’ and ‘preference rules’. Thus, for example, a durational pattern may allow for several equally plausible metric interpretations (as circumscribed by the well-formedness rules), but the choice of one metre in particular involves the application of their preference rules. The distinction between well-formedness and preference rules is one of Lerdahl and Jackendoff's most important contributions to music theory and analysis.
Lerdahl and Jackendoff's model has four basic components: grouping structure, metrical structure, time-span reduction and prolongational reduction (fig.1). Rhythm and pitch are given equal consideration, though they have different degrees of salience on different structural levels. Grouping extends from the foreground to the largest levels of formal structure. Metre, by contrast, is a foreground phenomenon, while time-span and prolongational structures emerge in the middleground and then extend to more background levels. In this fashion their theory includes both bottom-up and top-down components. Grouping in the foreground is concerned with the conjunction and articulation of successive sound-events based on Gestalt psychological principles (see §I, 3 above). Unlike groups that are defined in terms of relationships between strong and weak elements (as in Cooper and Meyer's approach), the generative theory does not specify the structural relationships between elements within a group. Rather, those relationships emerge from the interaction of grouping and metre (in the foreground) and grouping and time-span and prolongational structures at higher levels.
Rhythm, §III: Current rhythm research
The subject of rhythm and metre in serial and other non-tonal musics has received special attention from a number of theorists. One may wonder why a separate theory of post-tonal rhythm or metre is needed, but if one assumes that pitch structures are ontologically prior to rhythmic and metric structures, then in the absence of traditional tonal syntax one must seek an alternative source for rhythmic and metric organization. It is not surprising that many of the same theorists who embrace a Schenkerian pitch-to-rhythm approach in tonal contexts seek analogous sources for rhythm and metre in post-tonal musics. Hyde (F1984, p.25) characterizes the situation in the following way:
In tonal music, well-defined principles determine the equivalence or commensurability of pitch events and so regulate the articulation of rhythmic strata derived from them. These tonal principles – such as the rules of voice-leading and harmonic progression, or the role of triadic structure – can produce middleground pitch events that recur regularly, providing an important source of rhythmic accent. An analogous process operates in Schoenberg's twelve-tone music: structural principles determine analogous functions for various pitch events, recurrence of these analogous pitch events produces middleground rhythmic strata, and, as in tonal music, middleground strata make up a key source of rhythmic organization.
She goes on to say that the counterpart to those ‘tonal principles’ involves ‘unordered pitch-class sets that are equivalent to linear segments of the basic set’ and that these ‘secondary harmonic structures’ generate rhythmic and metric structures. Thus rhythmic and formal structures are determined by and/or seen as evidence of underlying pitch structures. Forte (F1983) has developed various techniques for uncovering rhythmic patterns, including a ‘proportional graph’ of the relative durations and an ‘attack-release partition’ of the composite rhythms of the musical surface. Using such techniques one may find structural correlations and moments of special structural import (such as durational symmetries) which in turn may guide the analyst's examination of pitch structures. Hasty (F1981, G1997) is also concerned with problems of segmentation, but approaches the question through a consideration of the essential aspects of motion and continuity as they occur in the music's unfolding, rather than those patterns which are the product of a final-state analysis.
Post-tonal rhythm has also been given attention from a compositional perspective, and to the extent that an analysis (and the music theory behind it) serves as an exegesis of compositional practice, the writings of contemporary composers are of interest. In extensions of serial technique duration, metre and so forth can either be yoked to the manipulations of the 12-note series itself, or themselves be subjected to analogous operations (see, for example, Krenek, F1960, and Babbitt, F1962–3). Outside a strictly serial context, rhythmic elements may be treated in the same way as pitch or pitch-class sets and arrays (e.g. Morris, 1987). In all these approaches essential isomorphisms between pitch and time are assumed to be present. For example, in her discussion of rhythmic contours Marvin (F1991), drawing on Morris (F1987), speaks of durational segments in ‘duration space’ which may be retrograded and/or inverted and compared in terms of various equivalence classes.
While such approaches to rhythmic structures may be useful as compositional techniques, their analytical application is not without its difficulties. First, if a mode of analysis proceeds in a pitch-to-rhythm fashion, then the determinative pitch structures must be apparent before rhythmic or metric parsing can begin. However, given that serial or set structures are not always (or even usually) aurally transparent, even to listeners with absolute pitch, their structural import would seem to emerge only through an analysis that takes scores, row matrices or set-type lists, and/or compositional sketches as a prerequisite. Even if row segments or unordered pitch-class sets are aurally discernible, they must also be distinctive enough to mark segment boundaries. Thus, for example, if the opening intervals of a given segment are common to a large variety of unordered pitch-class sets, then they will only weakly indicate the boundary between rhythmic segments, if at all. Investigations of rhythmic and metric discrimination in atonal contexts have found pitch cues to be of minimal salience (e.g. Clarke and Krumhansl, I1989–90). Another question concerns what features of a set or series of durations (or metric ordering) may be regarded as invariant under various operations. That is, we do not simply note the ‘durational content’ of a figure (e.g. ‘That figure contains three short, two medium and two long durations’) but rather attend to the durational transitions from short to long and so on as such transitions give a sense of movement and metre. One cannot, for example, reorder the continuously decreasing durations in an accelerando without wholly destroying the sense of tempo change. Similarly, Gjerdingen (I1992–3) reports that some real-time sequences of notes are heard in categorically different metres depending on whether they are heard in their ‘prime’ or ‘retrograde’ form.
Lewin's formalized approaches to post-tonal pitch and rhythm (F1981, F1984, F1987) show a clear awareness of the problems of directly applying pitch and pitch-class operations to rhythmic and metric elements. Lewin (F1987) presents a means of describing time-point and time-span relationships within the context of a generalized interval system (‘GIS’) that employs mathematical group theory. Lewin's goal is to add rigour to descriptions of musical relationships while preserving intuitions regarding pitch and temporal relationships. In the rhythmic domain he explores precedence relations for time-points, precedence relations in a metric context, proportional relationships among families of time-spans, equivalence classes among time-spans and durational patterns (i.e. augmentation and diminution, among other transformations), comparisons of duration as differences in length (in contrast to proportional relationships) and comparisons of duration in a modular duration-space. Lewin notes that his work has precedents and analogues in the compositional approaches developed by Babbitt, Carter and Stockhausen. His account of durational comparison – wherein, for example, a particular duration can be described as a ‘semibreve less a quaver’ or ‘a breve plus a crotchet’ – is very similar to the approach to rubato as ‘stolen time’ in various historical sources (see Hudson, H1994). Two of Lewin's observations regarding rhythm are particularly significant. The first is that any description (especially a formal one) of musical durations has non-trivial difficulties both in assigning a reference point in time by which durational succession, precedence and temporal interval can be regarded, and in choosing an integer unit of durational measurement. Lewin also notes that some of the rhythmic relationships he discusses are grounded in conceptual realms that do not accord well with musicians' experience of and intuitions about musical rhythm, and so must be used carefully in either composition or analysis.
Roeder (G1995) has developed a ‘calculus of accent’ which functions as a context-neutral approach to the determination of rhythmic stress. In his approach metre need not be present (though the presence of beats may be factored in); rather, changes in pitch contour and relative duration (peaks and valleys of pitch duration, as well as transitions from long to short durations and vice versa), along with other parameters, may be scaled and then used to give a formal account of relative stress. In this mode of analysis group boundaries are assumed to be known, and the goal is to fill in the degrees of accentedness among the members of a group. This also allows for comparison of the relative stress in different parameters – what Roeder calls a ‘polyphony of [accentual] attribute functions’ (p.39) – and avoids the artificial summation of ‘aggregate’ accents. Roeder's model does not require discrete pitches, so that he may (using integral calculus) produce accentual profiles in electronic and other musics which would ordinarily resist rhythmic analysis because they lack discrete durational elements and/or patterns.
Music theorists are not alone in developing formal approaches to rhythmic and metric analysis. As noted below, researchers in music cognition have developed algorithms for determining metric structure (in both final-state and real-time analyses), as well as formal descriptions of the timing and dynamics of real musical performances. While both groups pursue analogous research programmes, there are important differences. Music theorists, for the most part, employ formal theories of rhythm in order to deal with the rhythmic structure of post-tonal music. Theorists also typically use notated scores as the source of their data. These theorists are also often closely associated with compositional procedures and practices (and indeed may be composer-theorists or theorist-composers). Among cognitive scientists the emphasis is on the analysis of grouping, metre and/or accent in tonal music in order to create models that mimic listener behaviour. Moreover, much recent research by psychologists and cognitive scientists uses timing and dynamic information from live performances as the source of its data. Unfortunately, there has been little scholarly dialogue between music theorists and cognitive scientists who have explored formalized representations of rhythm and metre.
Rhythm, §III: Current rhythm research
Studies of musical rhythm go back to the 19th-century origins of modern psychology. Helmholtz, Wundt and their students examined basic thresholds of attention and discrimination in different sense modalities, which included the study of temporal discrimination in the auditory mode (see summaries in James, I1890). This research tradition has continued to the present day (though the observations of the earliest researchers have proved remarkably robust), and has established the basic constraints on sequential differentiation, preferred rates of attending, limits on successive integration and the psychological present, and so forth. Research in psychoacoustics has also yielded important results for studies of rhythm.
The most basic performance tests simply ask subjects to tap a series of beats spontaneously, or to tap along to a simple stimulus (see Fraisse, in Action and Perception, I1985, for a summary of earlier work). Such tests establish the upper and lower bounds for the production and maintenance of a beat, rate of tempo drift and so forth. Interestingly, they reveal little effect of musical training on basic beat-keeping abilities. In more complex contexts, however, including the perception and performance of polyrhythms (e.g. Handel and Oshinsky, I1981; Handel, I1983–4; and Grieshaber, H1990) and in passages that require subdivision (Yee and others, I1994), musically skilled subjects perform significantly better than non-musicians. The studies of polyrhythms also indicate that we do not hear ‘two rhythms at once’, but rather an integrated rhythmic/metric pattern, either by singling out one strand of the musical texture for attention (and ignoring others) or by constructing a composite rhythm from the various strands.
Judgment tasks have naturally focussed on musical attention and memory and their relation to rhythmic expectations. Jones (e.g. I1987, I1992) and her colleagues (Jones, Boltz and Kidd, I1982; Jones and Boltz, I1989; and Jones and Yee, I1993) have developed a dynamic model of attending which includes a metric component. Other studies (e.g. Dowling, Lung and Herrbold, I1987; and Gallun and Reisberg, I1994–5) have made use of interleaved melodies to study rhythmic attending. In such studies two familiar melodies (such as Mary had a little lamb and Yankee Doodle) are played in alternation, and while registral separation was important in allowing subjects to discern one (or both) of the melodies, metric position is also crucial. In this body of work an important consensus has emerged, namely that in the musical foreground structural judgments are made in a rhythm-to-pitch fashion, as metric position and grouping structure are the primary determinants of musical salience, while tonal considerations (scale degree, harmonization etc.) play a secondary role.
The earliest formal models for metre and rhythm used score-based data (equivalent to a ‘deadpan’ performance of the rhythmic patterns) and sought to identify downbeats and metric patterns using auto-correlation techniques which sought the onset(s) of the most common durational intervals (for a summary see Lee, I1991). Subsequent models, while still employing some form of auto-correlation, use real-time performance data as input. Desain and Honing (I1992) use a decompositional approach in designing their algorithm, a process that separately parses tempo tracking, metric period, downbeat location and so forth. They also employ a feed-forward component which mimics the anticipation of tempo, metre and grouping in established musical contexts (see also Rosenthal, I1988–9, I1992). Like Desain and Honing, Gjerdingen (I1989, I1992–3) makes use of neural network simulations to emulate human perception and performance. The ‘analysis by synthesis’ approach employs formalized theories of rubato, expressive variation and so forth to model expert musical performance (e.g. Friberg, Sundberg, and Frydén in Action and Perception, I1985; Gabrielsson, I1985–6; Sundberg, Friberg and Frydén, H1991–2). These performance models can then be used to generate stimuli which can be used in tests of perceptual acuity and/or aesthetic judgment. While some researchers have investigated the variations from ‘deadpan’ performance which characterize performance in a perceptually constant tempo (Clarke, I1989, H1992–3; Shaffer and Todd, I1994; and Sloboda, H1983), others have attempted to model rubato (Todd, H1989) and accelerandi and ritardandi (Desain and Honing, I1991; Epstein, H1995; and Feldman, Epstein and Richards, H1992–3) using techniques such as fitting tempo changes to cubic splines.
The growing attention to the timing and dynamics of music performed under concert conditions reflects a concern with the ecological validity of psychological measurement and experimental design. In more recent studies rhythm tends to be studied within the context of a pitch sequence (and vice versa), and indeed musical examples excerpted from the standard repertory are often used as stimulus materials. For example, Drake (I1993), Drake and Palmer (I1992–3), and Palmer and Krumhansl (I1990) have studied the interaction between tonal and durational components, what they refer to as the ‘joint accent structure’ of contour, durational, metric and tonal cues. This approach is not without its difficulties, as such stimuli often contain unwanted complications of metre, tonality and so forth. Nonetheless, such tests, using musical sounds (rather than, for example, a series of pure sinusoids) and realistic musical timing (rather than purely isochronous durations), have begun to give a richer picture of rhythmic perception and performance.
While a considerable amount of research in rhythmic perception and performance remains to be done, it is clear that in ecologically valid contexts musicians almost never perform durations, attacks and articulations as literally indicated in the score. The translation of a given notation into a sound-event involves a considerable amount of variation, even when contextual factors are taken into account. The performance and perception of musical rhythm are far more complex than musical notation would seem to allow, and present both problems and possibilities for the musicological study of rhythm and metre.
Rhythm, §III: Current rhythm research
As Langer noted: ‘Music makes time audible, and its form and continuity sensible. … It creates an image of time measured by the motion of forms that seem to give it substance, yet a substance that consists entirely of sound, so it is transitoriness itself’ (K1953, p.110). It is perhaps for this reason – music's seeming ability to make time effable – that philosophers who discuss time and temporality are drawn to examples and images from music. To listen to music is to engage with the phenomena of duration, succession and motion, and to describe that experience one must capture relations of past and present, and senses of being versus becoming.
Once a note has begun to sound we are aware of its continued duration – that we are hearing the same note (the same ‘event’) prolonged in time. How are we aware that time has passed? Most philosophers subscribe to the longstanding idea that an awareness of duration requires an awareness of change. Without a change in the configuration of our physical environment there can be no sense of time's passage, and so duration involves the continuation of some features of the environment measured against changes in others. This is the position taken by philosophers since Heraclitus and Plato (in the Timaeus). James noted that such change may be proprioceptic and located such awareness in the kinaesthetic system (I1890, p.620). From this perspective physical change is prior to our psychological awareness of duration. An alternative approach was offered by Bergson (K1911). As Čapek (K1971, p.89) noted, Bergson asserted the reality of the temporal first on the psychological level. Langer developed Bergson's thesis in a specifically musical context, where she spoke of the listener's awareness of ‘passage’ or a sense of transience, made manifest by fluctuations in physical, emotional and/or intellectual tensions.
When one is presented with series of notes, they are usually heard as a coherent and continuous entity, rather than as a succession of isolated moments. Such a series helps define the ‘psychological present’ or ‘specious present’ in which the present moment is not an instant but a span of some (albeit perhaps limited) duration. This concept goes back to James (I1890), who characterized the present as a ‘saddle back’ rather than a knife edge. James's concept of the present gives coherence to both an individual note – integrating its onset, continuation and conclusion – and a series of notes within a coherent ‘now’. Clifton (K1983), drawing on the work of Husserl, Heidegger and Merleau-Ponty, views the musical present as a nested sense of temporal contexts or ‘horizons’, including expectations of events yet to come (‘protentions’) as well as an awareness of what has occurred (‘retentions’) within which we structure our experience and knowledge of music (see also Ihde, K1976).
There is a dynamic quality to the succession of events within the musical present. For the transitions from note to note within a series of notes are not sensed as ‘state changes’ in our sonic environment, but rather as a species of motion. Philosophers such as Bergson (K1889, K1922) and Langer (K1953) saw this as a musical reflection of the essential nature of time. That is, time, especially time as made manifest in musical experience, is time-as-becoming as opposed to being-in-time. Hasty (G1997) argues that modes of description that treat musical rhythm and metre as static entities and patterns seriously distort the nature of the musical object. Drawing on the philosophical work of A.N. Whitehead (K1929) and the musicological work of Neumann (G1959), Hasty develops a projective theory of musical rhythm which aims to close the divide ‘between the fixity of what can be grasped as order in abstraction and the fluidity of a felt order in experience’ (p.3). Hasty feels this divide most keenly in the separation of metre and rhythm, an analytical premise that results in ‘our concept of meter [becoming] separated from our intuitions of rhythm as something fully temporal and processive’ (p.5).
Though most music affirms our sense of continuity and motion, many 20th-century pieces challenge or even deny the possibility of a coherent musical present as a compositional premise. Kramer (K1988) gives an extensive discussion of the various ways the horizons of the musical present may be distorted or broken in modern music and postmodern listening. He first distinguishes between musical linearity and non-linearity. Linearity is ‘the determination of some characteristic(s) of music in accordance with implications that arise from earlier events of the piece’ (p.20). Non-linearity, by contrast, is non-processive: ‘it is the determination of some characteristic(s) of music in accordance with implications that arise from principles or tendencies governing an entire piece or section’ (ibid.). Non-linearity is the antithesis of development. Linearity and non-linearity are not analogous to continuity and discontinuity. Discontinuities may arise in both linear and non-linear musical structures. Within the context of processive or goal-directed musical syntax we may find what Kramer terms ‘multiply directed’ linear time – a strategic reordering of a linear progression or linear process, such as beginning a piece with a cadential gesture. As an example of multiply directed linear time, Kramer gives an extended analysis of the first movement of Beethoven's op.135 (pp.123–36).
Beyond multiply directed linear time lies moment form. Stockhausen formulated the concept in an article which describes the compositional procedures involved in his Kontakte (see Stockhausen, Karlheinz). Moment forms ‘are forms in a state of always having already commenced, which could go on as they are for an eternity’ (Stockhausen, F1963, cited in Kramer, K1988, p.201). Moment forms stretch the horizons of the musical present to encompass the totality of each moment (which in some cases may be the entire piece). The elements of moment form are ‘self-contained entities, capable of standing on their own yet in some nonlinear sense belonging to the context of the composition’ (Kramer, K1988, p.207). Thus, if in a normal piece each event forms part of a larger tissue of protentions and retentions, building up a complex horizon that encircles the time-world of the piece, in moment form each section or element occurs within a self-contained horizon, a boundary that is impermeable to events that precede or follow. Pieces with a high degree of surface discontinuity and consisting of unfamiliar sounds (like much electronic music) are obvious examples of moment form. Music that uses the elements of tonal syntax may nonetheless be in moment form (see, for example, Kramer's analysis of Stravinsky's Symphonies of Wind Instruments, pp.221–81). While there may be a sense of temporal passage within (but not between) moments, in the most extreme cases even this sense of passage is lost. The result is a sense of stasis, or ‘vertical time’ in Kramer's terminology. Examples of pieces that create vertical time include Stockhausen's Stimmung, Rzewski's Les moutons de Panurge and Reich's Violin Phase. Vertical time is non-teleological, without any past retentions or future protentions impinging on one's experience of the sound event. The result is a collapse of the horizons of the moment down to a singularity, a single now.
Rhythm, §III: Current rhythm research
Musical traditions reflect the different temporal sensibilities of their respective ages. Before mechanical time-keepers were common, natural processes, especially the motions of the sun and stars, were seen as a source of temporal regularity and order. In those eras the metaphysics and ontology of time and motion are rooted in Platonic philosophy and Ptolemaic astronomy, where the primum mobile regulates all subsequent motion and where God is the true source of all time and motion, mirrored in musical thought and practice. The theory and notation of musical rhythm in the Middle Ages was similarly ‘top-down’ in its approach: all shorter values stemmed from systematic division of the perfect long.
The musical time-keeping of the Renaissance was manifest in the use of heartbeat, respiration and other physiological processes as the source for periodicity in nature – not in the stars, but in one's own body. The integer unit of time was cast on a human rather than cosmic scale. Perhaps also the presence of clocks and clockworks encouraged the notion that shorter as well as longer durations could exhibit constancy and regularity. Yet the era of great clock-making was not the Renaissance but the 17th and 18th centuries, from Galileo's discovery of the laws of pendular motion (1603) to Huygens's refinement of the pendular swing (1673). The age of reason was an age of greater and greater precision in time-keeping; it is during these decades that one finds a correspondingly greater degree of temporal control in music, culminating in the use of standard metronome markings in the first quarter of the 19th century. This culmination had its consequences, however. First, one finds a partial revolt through the greater use of rubato, or more precisely that rubato where one part of the texture remains constant (i.e. the left hand of the piano) while the other part pushes ahead and/or pulls behind the beat. In the 20th century the urge for rhythmic control met either with total success (as in complex multi-serial works and tape music) or with a move to complete anarchy (in aleatory compositions and performances). Thus our anxious age, when the most precise temporal control is possible, either in performance (with every player having a personal click track) or in recording, is also the era when music achieved the widest degree of temporal flexibility and freedom.
a: general histories, bibliographies
k: rhythm and temporal philosophy
A. Ruckmich: ‘A Bibliography of Rhythm’, American Journal of Psychology, xxiv (1913), 508; xxvi (1915), 457
T. Wiehmayer: Musikalische Rhythmik und Metrik (Magdeburg, 1917)
O. Bie: ‘Rhythm’, MQ, xi (1925), 331–8
G. Becking: Der musikalische Rhythmus als Erkenntnisquelle (Augsburg, 1928)
A. Verwey: Rhythmus und Metrum (Halle, 1934)
A. Arnholtz: Studier i poetisk og musikalisk rytmik, i (Copenhagen, 1938)
C. Alette: Theories of Rhythm (diss., U. of Rochester, NY, 1951)
J. Dunk: The Origin and Structure of Rhythm (London, 1952)
C. Höweler: Het rhythme in vers en muziek (The Hague, 1952)
J. Müller-Blattau: Das Verhältnis von Wort und Ton in der Geschichte der Musik: Grundzüge und Probleme (Stuttgart, 1952)
C. Sachs: Rhythm and Tempo (New York, 1953)
E. Willems: Le rythme musical: rythme, rythmique, métrique (Paris, 1954)
J. Bank: Tactus, Tempo, and Notation in Mensural Music from the 13th to the 17th Century (Amsterdam, 1972)
P. Righini: Studio analitico sul ritmo musicale e sue definizioni attraverso i secoli (Padua, 1972)
E. Apfel and C. Dahlhaus: Studien zur Theorie und Geschichte der musikalischen Rhythmik und Metrik (Munich, 1974)
W. Seidel: Rhythmus: eine Begriffsbestimmung (Darmstadt, 1976)
C. Bresgen: Im Anfang war der Rhythmus (Wilhelmshaven, 1977)
R. Rastall: The Notation of Western Music (New York, 1982)
E. Boal: Timepieces, Time, and Musical Tempo before 1700 (diss., Washington U., 1983)
G.L. Houle: Meter in Music, 1600–1800: Performance, Perception, and Notation (Bloomington, IN, 1987)
F. Neumann: ‘Conflicting Binary and Ternary Rhythms: from the Theory of Mensural Notation to the Music of J.S. Bach’, Music Forum, vi (1987), 93–128
M. Greene: Historical Precedents for Contemporary Theories of Musical Accent: a Study of Rhythmic Theories from Kirnberger to the Present (diss., U. of Chicago, 1991)
S.L. Macey, ed.: Encyclopedia of Time (New York, 1994)
Aristides Quintilianus: Peri mousikēs [On music] (MS, c200); ed. and trans. T.J. Mathiesen, Aristides Quintilianus On Music in Three Books (New Haven, CT, 1983)
Johannes de Garlandia: ‘Ars rithmica’, De mensurabili musica (MS, c1240); trans T. Lawler (New Haven, CT, 1974)
R. Westphal: Griechische Rhythmik und Harmonik nebst der Geschichte der drei musicalischen Disziplinen (Leipzig, 1867)
R. Westphal: Aristoxenos von Tarent: Melik und Rhythmik des classischen Hellenentums (Leipzig, 1883–93/R)
G. Mari: ‘I trattati medievali di ritmica latina’, Memorie del Reale Istituto Lombardo di scienze e lettere: Classe di lettere, scienze storiche e morali, xx (Milan, 1899), 373–496
W. Meyer: Gesammelte Abhandlungen zur mittellateinischen Rhythmik (Berlin, 1905–36/R)
C. Williams: The Aristoxenian Theory of Musical Rhythm (Cambridge, 1911)
J.G. Schmidt, ed.: Haupttexte der gregorianischen Autoren betreffs Rhythmus (Düsseldorf, 1921)
A. Michalitschke: Theorie des Modus (Regensburg, 1923)
K.G. Fellerer: Die Deklamationsrhythmik in der vokalen Polyphonie des 16. Jahrhunderts (Düsseldorf, 1928)
E. Jammers: Der gregorianische Rhythmus: antiphonale Studien (Leipzig, 1937)
T. Georgiades: Der griechische Rhythmus: Musik, Reigen, Vers und Sprache (Tutzing, 1949)
F. Gennrich: ‘Grundsätzliches zur Rhythmik der mittelalterlichen Monodie’, Mf, vii (1954), 150–76
H. Husmann: ‘Das System der modalen Rhythmik’, AMw, xi (1954), 1–38
W. Waite: The Rhythm of Twelfth-Century Polyphony: its Theory and Practice (New Haven, CT, 1954/R)
F. de Meeûs: ‘Le problème de la rythmique grégorienne, à propos de travaux récents’, AcM, xxviii (1956), 164–75
R. Monterosso: Musica e ritmica dei trovatori (Milan, 1956)
R. Crocker: ‘Musica rhythmica and Musica metrica in Antique and Medieval Theory’, JMT, ii (1958), 2–23
T. Georgiades: Musik und Rhythmus bei den Griechen (Hamburg, 1958)
G. Murray: ‘The Authentic Rhythm of Gregorian Chant’, Caecilia, lxxxvi (1959), 57–71
J. Vollaerts: Rhythmic Proportions in Early Medieval Ecclesiastical Chant (Leiden, 2/1960)
B. Kippenberg: Der Rhythmus im Minnesang: eine Kritik der literar- und musikhistorischen Forschung (Munich, 1962)
E. Sanders: ‘Duple Rhythm and Alternate Third Mode in the 13th Century’, JAMS, xv (1962), 249–91
J. Rayburn: Gregorian Chant Rhythm: a History of the Controversy concerning its Interpretation (New York, 1964)
Andrew Hughes: ‘Mensuration and Proportion in Early Fifteenth Century English Music’, AcM, xxxvii (1965), 48–59
H. Vanderwerf: ‘Deklamatorischer Rhythmus in den Chansons der Trouvères’, Mf, xx (1967), 122–44
S. Baud-Bovy: ‘Equivalences métriques dans la musique vocale grecque antique et moderne’, RdM, liv/1 (1968), 3–15
A. Mendel: ‘Some Ambiguities of the Mensural System’, Studies in Music History: Essays for Oliver Strunk, ed. H. Powers (Princeton, NJ, 1968), 137–60
R. Erickson: Rhythmic Problems and Melodic Structure in Organum Purum: a Computer-Assisted Study (diss., Yale U., 1970)
T. Karp: ‘Rhythmic Architecture in the Music of the High Middle Ages’, Medievalia et humanistica, i (1970), 67–80
H. Van der Werf: ‘Concerning the Measurability of Medieval Music’, CMc, no.10 (1970), 69–73
W. Anderson: ‘Word-Accent and Melody in Ancient Greek Musical Texts’, JMT, xvii (1973), 186–203
P. Gossett: ‘The Mensural System and the “Choralis Constantinus”’, Studies in Renaissance and Baroque Music in Honor of Arthur Mendel, ed. R.L. Marshall (Kassel and Hackensack, NJ, 1974), 71–107
E. Jammers: ‘Gregorianischer Rhythmus, was ist das?’, AMw, xxxi (1974), 290–311
H. Tischler: ‘Rhythm, Meter, and Melodic Organization in Medieval Song’, RBM, xxviii–xxx (1974–6), 5–23
B. Gillingham: ‘Modal Rhythm and the Medieval Sequence’, SMC, i (1976), 105–23
B. Antley: The Rhythm of Medieval Music: a Study in the Relationship of Stress and Quantity and a Theory of Reconstruction with a Translation of John of Garland's ‘De mensurabili musica’ (diss., Florida State U., 1977)
J. Knapp: ‘Musical Declamation and Poetic Rhythm in an Early Layer of Notre Dame Conductus’, JAMS, xxxii (1979), 383–407
L. Rowell: ‘Aristoxenus on Rhythm’, JMT, xxiii (1979), 63–79
L. Treitler: ‘Regarding Meter and Rhythm in the Ars Antiqua’, MQ, lxv (1979), 524–58
E. Sanders: ‘Consonance and Rhythm in the Organum of the 12th and 13th Centuries’, JAMS, xxxiii (1980), 264–86
H. Tischler: ‘Apropos Meter and Rhythm in the Ars Antiqua’, JMT, xxvi (1982), 313–29 [see also L. Treitler, JMT, xxvii (1983), 215–22]
J. Yudkin: ‘The Rhythm of Organum Purum’, JM, ii (1983), 355–76
T. Mathiesen: ‘Rhythm and Meter in Ancient Greek Music’, Music Theory Spectrum, vii (1985), 159–80
E. Sanders: ‘Conductus and Modal Rhythm’, JAMS, xxxviii (1985), 439–69
B. Gillingham: Modal Rhythm (Ottawa, 1986)
M. Fassler: ‘Accent, Meter, and Rhythm in Medieval Treatises “De rithmis”’, JM, v (1987), 164–90
R. Crocker: ‘Rhythm in Early Polyphony’, CMc, nos.45–7 (1990), 147–77
E.H. Roesner: ‘The Emergence of Musica Mensurabilis’, Studies in Musical Sources and Styles: Essays in Honor of Jan LaRue, ed. E.K. Wolf and E.H. Roesner (Madison, WI, 1990), 41–74
C. Turner: ‘Proportion and Form in the Continental Isorhythmic Motet c. 1385–1450’, MAn, x (1991), 89–124
A.M.B. Berger: Mensuration and Proportion Signs: Origins and Evolution (Oxford, 1993)
W. Seidel: ‘Rhythmus/numerus’ (1994), HMT
E. Sanders: ‘Rithmus’, Essays on Medieval Music in Honor of David G. Hughes, ed. G.M. Boone (Cambridge, MA, 1995), 415–40
M. Bent: ‘The Early Use of the Sign O’, EMc, xxiv (1996), 199–225
MersenneHU
B. Ramos de Pareia: Musica practica (Bologna, 1482/R); Eng. trans., MSD, xliv (1993)
Adam von Fulda: De musica (MS, 1490); ed. in GerbertS, iii, 329
F. Gaffurius: Practica musice (Milan, 1496/R); Eng. trans., MSD, xx (1969)
H. Buchner: Fundamentum (MS, c1520); ed. in VMw, v (1889), 1–192
G. Diruta: Il transilvano (Venice, 1593–1609/R); ed. M. Bradshaw and E.J. Soehnlen (Henryville, PA, 1984)
W. Printz: Compendium musicae signatoriae et modulatoriae vocalis (Dresden, 1689/R, 2/1714)
G. Muffat: Florilegium secundum (Passau, 1698/R); ed. in DTÖ, iv, Jg.ii/2 (1895/R)
J. Heinichen: Der General-Bass in der Composition (Dresden, 1728/R)
J. Mattheson: Der vollkommene Kapellmeister (Hamburg, 1739/R; Eng. trans., 1981)
J. Quantz: Versuch einer Anweisung die Flöte traversière zu spielen (Berlin, 1752/R, 3/1759/R; Eng. trans., 1985)
A. Orel: ‘Zur Frage der rhythmischen Qualität in Tonsätzen des 15. Jahrhunderts’, ZMw, vi (1923–4), 559–607
P. Radcliffe: ‘The Relation of Rhythm and Tonality in the 16th Century’, PRMA, lvii (1930–31), 73–97
E. Jammers: ‘Die Barockmusik und ihre Stellung in der Entwicklungsgeschichte des Rhythmus’, Festschrift Martin Bollert zum 60. Geburtstage, ed. H. Neubert (Dresden, 1936), 255–78
A. Einstein: ‘Narrative Rhythm in the Madrigal’, trans. W. Wager, MQ, xxix (1943), 475–84
S. Babitz: ‘A Problem of Rhythm in Baroque Music’, MQ, xxxviii (1952), 533–65
F.-J. Machatius: Die Tempi in der Musik um 1600 (diss., Freiz Universität, Berlin, 1952)
H. Heckmann: ‘Der Takt in der Musiklehre des 17. Jahrhunderts’, AMw, x (1953), 116–39
F. Rothschild: The Lost Tradition in Music: Rhythm and Tempo in the Time of J.S. Bach (London, 1953)
H. Zingerle: Zur Entwicklung der Rhythmik und Textbehandlung in der Chanson von ca. 1470–1530 (Innsbruck, 1954)
S. Goldthwaite: Rhythmic Patterns and Formal Symmetry in the Fifteenth-Century Chanson (diss., Harvard U., 1955)
M. Burton: Changing Concepts of Rhythm in English Musical Writings, 1500–1700 (diss., U. of Rochester, NY, 1956)
C. Dahlhaus: ‘Zur Theorie des Tactus im 16. Jahrhundert’, AMw, xvii (1960), 22–39
C. Dahlhaus: ‘Zur Entstehung des modernen Taktsystems im 17. Jahrhundert’, AMw, xviii (1961), 223–40
C. Jacobs: Tempo Notation in Renaissance Spain (Brooklyn, NY, 1964)
A. Auda: Théorie et pratique du tactus (Brussels, 1965)
P. Aldrich: Rhythm in Seventeenth-Century Italian Monody (New York, 1966)
L. Schrade: ‘Über die Natur des Barockrhythmus’, De scientia musicae studia atque orationes, ed. E. Lichtenhahn (Berne, 1967), 360–84
W. Kümmel: ‘Zum Tempo in der italienischen Mensuralmusik des 15. Jahrhunderts’, AcM, xlii (1970), 150–63
J. Casell: Rhythmic Inequality and Tempo in French Music between 1650 and 1740 (diss., U. of Minnesota, 1973)
H. Wolff: ‘Das Tempo der französischen Musik um und nach 1700’, Musica, xxvii (1973), 452–3
R. Court: ‘Rythme, tempo, mesure’, Revue d'esthétique, xxvii/2 (1974), 143–59
E. Houghton: ‘Rhythm and Meter in 15th-Century Polyphony’, JMT, xviii (1974), 190–212
A. Planchart: ‘Tactus, Tempo and Notation in Mensural Music from the 13th to the 17th Century’, JMT, xix (1975), 154–60
E. Schroeder: ‘The Stroke Comes Full Circle: the Sign of Perfect Tempus and the Sign of Imperfect Tempus in Writings on Music C1450–1540 (Tempo Relationships in Notation)’, MD, xxxvi (1982), 119–66
S. Maier: Studien zur Theorie des Taktes in der 1. Halfte des 18. Jahrhunderts, (Tutzing, 1984)
W. Horn: ‘Johann David Heinichen und die musikalische Zeit: die Quantitas intrinseca und der Begriff des Akzenttakts’, Musiktheorie, vii/3 (1992), 195–218
S.E. Hefling: Rhythmic Alteration in Seventeenth- and Eighteenth-Century Music: Notes inégales and Overdotting (New York, 1993)
J. Riepel: Anfangsgründe zur musikalischen Setzkunst: nicht zwar altmathematischer Einbildungsart der Zirkel-Harmonisten, sondern durchgehends mit sichtbaren Exempeln abgefasset (Frankfurt, Leipzig and Augsburg, 1752–68)
H. Koch: Versuch einer Anleitung zur Composition (Leipzig, 1782–93/R; Eng. trans., 1983)
F. Thiémé: Nouvelle théorie sur les différens mouvemens des airs fondée sur la pratique de la musique moderne, avec le projet d'un nouveau chronométre (Paris, 1801)
J.-J. Momigny: Cours complet d'harmonie et de composition (Paris, 1803–6, 2/1808)
C. Mason: Rules on the Times, Metres, Phrases and Accent of Composition (London, 1806)
G. Weber: Versuch einer geordneten Theorie der Tonsetzkunst (Mainz, 1817–21, 3/1832; Eng. trans., 1851)
M. Hauptmann: Die Natur der Harmonik und der Metrik, ed. O. Paul (Leipzig, 1853, 2/1873; Eng. trans., 1888/R)
M. Lussy: Traité de l'expression musicale: accents, nuances et mouvements dans la musique vocale et instrumentale (Paris, 1873, 3/1877)
H. Riemann: Musikalische Syntaxis (Leipzig, 1877)
H. Riemann: Musikalische Dynamik und Agogik: Lehrbuch der musikalischen Phrasierung (Hamburg, 1884)
H. Lussy: ‘Die Correlation zwischen Takt und Rhythmus’, VMw, i (1885), 141–57
H. Riemann: System der musikalischen Rhythmik und Metrik (Leipzig, 1903/R)
H. Riemann: ‘Ein Kapitel vom Rhythmus’, Die Musik, iii/3 (1903–4), 155–62
A. Feil: Satztechnische Fragen in den Kompositionslehren von F.E. Niedt, J. Riepel, und H.C. Koch (Heidelberg, 1955)
H. Smither: Theories of Rhythm in the Nineteenth and Twentieth Centuries (diss., Cornell U., 1960)
M. Rothärmel: Der musikalische Zeitbegriff seit Moritz Hauptmann (Regensburg, 2/1968)
A. Palm: Jérôme-Joseph de Momigny: Leben und Werk (Cologne, 1969)
P. Aldrich: ‘“Rhythmic Harmony” as Taught by Johann Philipp Kirnberger’, Studies in Eighteenth-Century Music: a Tribute to Karl Geiringer, ed. H.C.R. Landon and R. Chapman (New York and London, 1970), 37–52
G. Henneberg: Theorien zur Rhythmik und Metrik: Möglichkeiten und Grenzen rhythmischer und metrischer Analyse, dargestellt am Beispiel der Wiener Klassik (Tutzing, 1974)
W. Seidel: Über Rhythmustheorien der Neuzeit (Berne, 1975)
N. Baker: ‘Heinrich Koch and the Theory of Melody’, JMT, xx (1976), 1–48
W. Caplin: ‘Harmony and Meter in the Theories of Simon Sechter’, Music Theory Spectrum, ii (1980), 74–89
W. Caplin: Theories of Harmonic-Metric Relationships from Rameau to Riemann (diss., U. of Chicago, 1981)
W. Allanbrook: Rhythmic Gesture in Mozart (Chicago, 1983)
P. Tenhaef: Studien zur Vortragsbezeichnung in der Musik des 19. Jahrhunderts (Kassel, 1983)
W. Caplin: ‘Hugo Riemann's Theory of “Dynamic Shading”: a Theory of Musical Meter?’, Theoria, i (1985), 1–24
F. Grave: ‘Metrical Displacement and the Compound Measure in Eighteenth-Century Theory and Practice’, Theoria, i (1985), 25–60
H. Macdonald: ‘[G flat major]’, 19CM, xi (1987–8), 231–7
C. Dahlhaus: ‘Zum Taktbegriff der Wiener Klassik’, AMw, xlv (1988), 1–15
I. Waldbauer: ‘Riemann's Periodization Revisited and Revised’, JMT, xxxiii (1989), 333–91
M. Kugler: ‘Die Begriffe Rhythmus und Rhythmik bei Riemann, Lussy und Jaques-Dalcroze: zur Unterscheidung des musikpädagogischen vom musikwissenschaftlichen Verständnis von Fachbegriffen’, Zur Terminologie in der Musikpädagogik (Mainz, 1991), 58–84
A. Feil: ‘Zum Rhythmus der Wiener Klassiker’, GfMKB: Baden, nr Vienna, 1991, 241–54
L. Klages: Vom Wesen des Rhythmus (Kampen auf Sylt, 1934)
E. Schmidt: Über den Aufbau rhythmischer Gestalten (Munich, 1939)
E. Toch: The Shaping Forces in Music (New York, 1948/R)
H. Leichtentritt: Musical Form (Cambridge, MA, 1951)
G. Cooper and L. Meyer: The Rhythmic Structure of Music (Chicago, 1960)
I. Bengtsson: ‘On the Relationship between Tonal and Rhythmic Structures in Western Multipart Music’, STMf, xliii (1961), 49–76
J. Schillinger: Encyclopedia of Rhythms: … a Massive Collection of Rhythm Patterns … Arranged in Instrumental Form (New York, 1966/R)
E. Cone: Musical Form and Musical Performance (New York, 1968)
A. Pierce: The Analysis of Rhythm in Tonal Music (diss., Brandeis U., 1968)
R. Westphal: Allgemeine Theorie der musikalischen Rhythmik seit J.S. Bach (Wiesbaden, 1968)
R. Morgan: The Delayed Structural Downbeat and its Effect on the Tonal and Rhythmic Structure of Sonata Form Recapitulation (diss., Princeton U., 1969)
K. Hławiczka: ‘Musikalischer Rhythmus und Metrum’, Mf, xxiv (1971), 385–406
A. Komar: Theory of Suspensions (Princeton, NJ, 1971)
L. Meyer: Explaining Music (Chicago, 1973)
P. Westergaard: An Introduction to Tonal Theory (New York, 1975), 225–410
C. Dahlhaus: ‘Polemisches zur Theorie der Musikalischen Rhythmik und Metrik’, Mf, xxviii (1976), 183–6
C. Kaden: ‘Strukturelle Segmentierung von Musik: Probleme, Schwierigkeiten, Möglichkeiten’, BMw, xviii (1976), 149–62, 293–334
K. Mehner: Grundfragen einer Theorie des musikalischen Rhythmus (diss., Humboldt U., 1976)
C. Schachter: ‘Rhythm and Linear Analysis: a Preliminary Study’, Music Forum, iv (1976), 281–334
M. Yeston: The Stratification of Musical Rhythm (New Haven, CT, 1976)
V. Holopova: Problemy muzïkal'nogo ritma (Moscow, 1978)
R. Morgan: ‘The Theory and Analysis of Tonal Rhythm’, MQ, lxiv (1978), 435–73
D. Epstein: Beyond Orpheus (Cambridge, MA, 1979)
J. Lester: ‘Articulation of Tonal Structures as a Criterion for Analytic Choices’, Music Theory Spectrum, i (1979), 67–79
J. Lochhead: ‘The Temporal in Beethoven's Opus 135: When are Ends Beginnings?’, In Theory Only, iv (1979), 3–30
C. Schachter: ‘Rhythm and Linear Analysis: Durational Reduction’, Music Forum, (1980), 197–232
W. Rothstein: Rhythm and the Theory of Structural Levels (diss., Yale U., 1981)
F. Lerdahl and R. Jackendoff: A Generative Theory of Tonal Music (Cambridge, MA, 1983)
M. Holcomb: Rhythmic Theories in Schenkerian Literature: an Alternative View (diss., U. of Texas, 1984)
J. Peel and W. Slawson: ‘A Generative Theory of Tonal Music’, JMT, xxviii (1984), 271–94 [review]
E. Cone: ‘Musical Form and Musical Performance Reconsidered’, Music Theory Spectrum, vii (1985), 148–58
E. Hantz: ‘A Generative Theory of Tonal Music’, Music Theory Spectrum, vii (1985), 190–202 [review]
N. Wick: A Theory of Rhythmic Levels in Tonal Music (diss., U. of Wisconsin, 1986)
J. Lester: The Rhythms of Tonal Music (Carbondale, IL, 1986)
M. Baker: ‘A Computational Approach to Modeling Musical Grouping Structure’, CMR, iv (1989), 311–25
W. Rothstein: Phrase Rhythm in Tonal Music (New York, 1989)
A. Cadwallader, ed.: Trends in Schenkerian Research (New York, 1990)
R. Graybill: ‘Towards a Pedagogy of Gestural Rhythm’, Journal of Music Theory Pedagogy, iv (1990), 1–50
E. Narmour: The Analysis and Cognition of Basic Melodic Structures (Chicago, 1990)
D. Smyth: ‘Large-Scale Rhythm and Classical Form’, Music Theory Spectrum, xii (1990), 236–46
L.B. Meyer: ‘A Pride of Prejudices; or, Delight in Diversity’, Music Theory Spectrum, xiii (1991), 241–51
N. Schneider: Die Kunst des Teilens: Zeit, Rhythmus und Zahl (Munich, 1991)
L. Zbikowski: Large-Scale Rhythm and Systems of Grouping (diss., Yale U., 1991)
E. Narmour: The Analysis and Cognition of Melodic Complexity: the Implication-Realization Model (Chicago, 1992)
M. Botelho: Rhythm, Meter, and Phrase: Temporal Structures in Johann Sebastian Bach's Concertos (diss., U. of Michigan, 1993)
C. Brower: Motion in Music: a Wave Model of Rhythm (diss., U. of Cincinnati, 1993)
R. Saltini: Theory of Phase Shift: Study of Rhythmic and Metric Displacements in Music (diss., SUNY, 1994)
B. Taggart: Rhythmic Perception and Conception: Study of Bottom-Up and Top-Down Interaction in Rhythm and Meter (diss., U. of Pennsylvania, 1996)
J. London: ‘Lerdahl and Jackendoff's Strong Reduction Hyphothesis and the Limits of Analytical Description’, In Theory Only, xiii (1997), 3–28
C. Willner: ‘Stress and Counterstress: Accentual Conflict and Reconciliation in J.S. Bach's Instrumental Works’, Music Theory Spectrum, xx (1998), 280–304
F. Samarotto: ‘Strange Dimensions: Regularity and Irregularity in Deep Levels of Rhythmic Reductions’, Schenker Studies, ii, ed. C. Schachter and H. Siegel (Cambridge, 1999)
VintonD (H. Smither, F. Rzewski)
O. Messiaen: Technique de mon langage musical (Paris, 1944; Eng. trans., 1957)
W. Austin: Harmonic Rhythm in Twentieth-Century Music (diss., Harvard U., 1951)
B. Blacher: ‘Über variable Metrik’, ÖMz, vi (1951), 219–22
R. Sessions: Harmonic Practice (New York, 1951)
E. Carter: ‘The Rhythmic Basis of American Music’, The Score, no.12 (1955), 27–32
K. Hławiczka: ‘Die rhythmische Verwechslung’, Mf, xi (1958), 33–49
F. Attneave: ‘Stochastic Composition Process’, Journal of Aesthetics and Art Criticism, xvii (1959), 503–10
K. Stockhausen: ‘How Time Passes’, Die Reihe, iii (1959), 10–40
K. Stockhausen: ‘Structure and Experiential Time’, Die Reihe, ii (1959), 64–74
E. Krenek: ‘Extents and Limits of Serial Technique’, MQ, xxxvi (1960), 210–32
J. Cage: Silence, ed. G. Kepes (Cambridge, MA, 1961)
M. Babbitt: ‘Twelve-Tone Rhythmic Structure and the Electronic Medium’, PNM, i/1 (1962–3), 49–79
P. Westergaard: ‘Some Problems in Rhythmic Theory and Analysis’, PNM, i/1 (1962–3), 180–91
P. Boulez: Musikdenken heute (Mainz, 1963; Fr. orig., Paris, 1964, as Penser la musique aujourd'hui; Eng. trans., 1971, as Boulez on Music Today)
R. Erickson: ‘Time-Relations’, JMT, vii (1963), 174–92
K. Stockhausen: Texte zur elektronischen und instrumentalen Musik, i (Cologne, 1963)
H. Smither: ‘The Rhythmic Analysis of Twentieth-Century Music’, JMT, viii (1964), 54–88
C. Dahlhaus: ‘Probleme des Rhythmus in der neuen Musik’, Zur Terminologie der neuen Musik (Berlin, 1965)
J. Cage: ‘Rhythm, etc’, Module, Proportion, Symmetry, Rhythm, ed. G. Kepes (New York, 1966), 194–203
H. Weinberg: A Method of Transferring the Pitch Organization of a Twelve Tone Set through all Layers of a Composition: a Method of Transforming Rhythmic Content through Operations Analogous to those of the Pitch Domain (diss., Princeton U., 1966)
E. Varèse: ‘Rhythm, Form, and Content’, Contemporary Composers on Contemporary Music, ed. E. Schwartz and B. Childs (New York, 1967), 201–4
V. Holopova: [The problem of rhythm in the work of composers of the first half of the 20th century] (Moscow, 1971)
J. Little: Architectonic Levels of Rhythmic Organization in Selected Twentieth-Century Music (diss., Indiana U., 1971)
I. Xenakis: Formalized Music (Bloomington, IN, 1971)
H. Pousseur: ‘The Question of Order in New Music’, Perspectives on Contemporary Music Theory, ed. B. Boretz and E.T. Cone (New York, 1972), 97–115
J. Rahn: ‘On Pitch or Rhythm: Interpretation of Orderings in Pitch and Time’, PNM, xiii (1974–5), 182–203
A. Winold: ‘Rhythm in Twentieth-Century Music’, Aspects of Twentieth-Century Music, ed. G.E. Wittlich (Englewood Cliffs, NJ, 1975), 208–69
B. Childs: ‘Time and Music: a Composer's View’, PNM, xv/2 (1976–7), 194–220
J. Rahn: ‘Rhythm, and Talk about it’, PNM, xv/2 (1976–7), 235–8
E. Carter: ‘Music and the Time Screen’, The Writings of Elliott Carter, ed. E. and K. Stone (Bloomington, IN, 1977), 343–65
R. Howat: ‘Debussy, Ravel and Bartók: Towards Some New Concepts of Form’, ML, lviii (1977), 285–93
J. Rahn: ‘Evaluating Metrical Interpretations’, PNM, xvi (1977–8), 35–49
E. Haimo: ‘Rhythmic Theory and Analysis’, In Theory Only, iv (1978), 18–35
J. Kramer: ‘Moment Form in Twentieth-Century Music’, MQ, liv (1978), 177–94
C. Wuorinen: Simple Composition (New York, 1979)
A. Forte: ‘Aspects of Rhythm in Webern's Atonal Music’, Music Theory Spectrum, ii (1980), 90–109
R. Hilmar: ‘Metrische Proportionen und serielle Rhythmik im “Kammerkonzert” von Alban Berg’, SMz, cxx (1980), 355–60
W. Johnson: Time-Point Sets and Meter (diss., Princeton U., 1980)
D. Lewin: ‘On Generalized Intervals and Transformations’, JMT, xxiv (1980), 243–51
C. Hasty: ‘Rhythm in Post-Tonal Music: Preliminary Questions of Duration and Motion’, JMT, xxv (1981), 183–216
D. Lewin: ‘Some Investigations into Foreground Rhythmic and Metric Patterning’, Music Theory: Special Topics, ed. R. Browne (New York, 1981), 101–37
J. Kramer: ‘New Temporalities in Music’, Critical Inquiry, vii (1981–2), 539–56
G. Brodhead: Structural Time in Twentieth-Century Tonal Music (diss., Indiana U., 1983)
A. Forte: ‘Foreground Rhythm in Early Twentieth-Century Music’, MAn, ii (1983), 239–68
R. Howat: Debussy in Proportion (Cambridge, 1983)
E. Lendvai: The Workshop of Bartók and Kodály (Budapest, 1983)
P. van den Toorn: ‘Rhythmic (or Metric) Invention’, The Music of Igor Stravinsky (New Haven, CT, 1983), 204–51
W. Johnson: ‘Time Point Sets and Meter’, PNM, xxii (1983–4), 278–95
M. Hyde: ‘A Theory of Twelve-Tone Meter’, Music Theory Spectrum, vi (1984), 14–51
D. Lewin: ‘On Formal Intervals between Time-Spans’, Music Perception, i (1984), 414–23
J. Lester: ‘Notated and Heard Meter’, PNM, xxiv (1985–6), 116–28
C. Hasty: ‘On the Problem of Succession and Continuity in Twentieth-Century Music’, Music Theory Spectrum, viii (1986), 58–74
J. Lochhead: ‘Temporal Structure in Recent Music’, JMR, vi (1986), 49–93
P. Lusson: ‘Place d'une théorie générale du rythme parmi les théories analytiques contemporaines’, Analyse musicale, ii (1986), 44–51
D. Lewin: Generalized Musical Intervals and Transformations (New Haven, CT, 1987)
R.D. Morris: Composition with Pitch Classes (New Haven, CT, 1987)
J. Bernard: ‘The Evolution of Elliott Carter's Rhythmic Practice’, PNM, xxvi (1988), 164–203
E. Marvin: A Generalized Theory of Musical Contour: its Application to Melodic and Rhythmic Analysis of Non-Tonal Music and its Perceptual and Pedagogical Implications (diss., U. of Rochester, NY, 1989)
I. Xenakis: ‘Concerning Time’, PNM, xxvii (1989), 84–93
B. Marvin: ‘The Perception of Rhythm in Non-Tonal Music: Rhythmic Contours in the Music of Edgard Varèse’, Music Theory Spectrum, xiii (1991), 61–78
A. Pierce: ‘An Advance on a Theory for all Music: At-Least-As Predicates for Pitch, Time, and Loudness’, PNM, xxx (1992), 158–83
E. Agmon: ‘Musical Durations as Mathematical Intervals: Some Implications for the Theory and Analysis of Rhythm’, MAn, xvi (1997), 45–75
P. Nauert: Timespan Formation in Nonmetric, Post-Tonal Music (diss., Columbia U., 1997)
E. Levy: ‘Von der Synkope: ein Beitrag zur Metrik und Rhythmik’, Festschrift Karl Nef zum 60. Geburtstag (Zürich, 1933), 150–56
J. Kunst: Metre, Rhythm, Multi-Part Music (Leiden, 1950)
V. Zuckerkandl: Sound and Symbol: Music and the External World, trans. W.R. Trask (New York, 1956)
K. Hławiczka: ‘Die rhythmische Verwechslung’, Mf, xi (1958), 33–49
F. Neumann: Die Zeitgestalt: ein Lehre vom musikalischen Rhythmus (Vienna, 1959)
K. Hławiczka: ‘Musikalischer Rhythmus und Metrum’, Mf, xxiv (1971), 385–406
A. Imbrie: ‘Extra Measures and Metrical Ambiguity in Beethoven’, Beethoven Studies, ed. A. Tyson (London, 1973), 44–66
J. Graziano: A Theory of Accent in Tonal Music of the Classic-Romantic Period (diss., Yale U., 1975)
R. Ricci: ‘The Division of the Pulse: Progressive and Retrogressive Rhythmic Forces’, In Theory Only, i (1975), 13–19
W. Berry: Structural Functions in Music (Englewood Cliffs, NJ, 1976), 301–424
W. Caplin: ‘Der Akzent des Anfangs: zur Theorie des musikalischen Taktes’, Zeitschrift für Musiktheorie, ix (1978), 17–28
W.E. Benjamin: ‘A Theory of Musical Meter’, Music Perception, i (1984), 355–413
W. Berry: ‘Metric and Rhythmic Articulation in Music’, Music Theory Spectrum, vii (1985), 7–33
H. Krebs: ‘Some Extensions of the Concepts of Metrical Consonance and Dissonance’, JMT, xxxi (1987), 99–120
C. Schachter: ‘Rhythm and Linear Analysis: Aspects of Meter’ Music Forum, vi (1987), 1–59
M. Botelho: ‘Meter and the Play of Ambiguity in the Third Brandenburg Concerto’, In Theory Only, xi (1990), 1–36
W. Frisch: ‘The Shifting Bar Line: Metric Displacement in Brahms’, Brahms Studies, ed. G. Bozarth (Oxford, 1990), 139–63
J.M. London: ‘Metric Ambiguity (?) in Bach's Brandenburg Concerto Number 3’, In Theory Only, vii (1991), 21–54
R. Cohn: ‘Metric and Hypermetric Dissonance in the Menuetto of Mozart's Symphony in G-minor, K. 550’, Integral, vi (1992), 1–33
H. Krebs: ‘Review of William Rothstein: Phrase Rhythm in Tonal Music and Carl Schachter: Three Articles in “Rhythm and Analysis”’, Music Theory Spectrum, xiv (1992), 82–7
R. Cohn: ‘The Dramatization of Hypermetric Conflicts in the Scherzo of Beethoven's Ninth Symphony’, 19CM, xv (1992–3), 188–206
R. Kamien: ‘Conflicting Metrical Patterns in Accompaniment and Melody in Works by Mozart and Beethoven: a Preliminary Study’, JMT, xxvii (1993), 311–48
J.M. London: ‘Loud Rests and Other Strange Metric Phenomena’, Music Theory Online (1993) 〈www.smt.ucsb.edu/mto>
H. Meltzer: Private Time and Public Time: Rhythm and Meter in Wagner's ‘Tristan und Isolde’ (diss., Columbia U., 1994)
F. Grave: ‘Metrical Dissonance in Haydn’, JM, xii (1995), 168–202
J.M. London: ‘Some Examples of Complex Meters and their Implications for Models of Metric Perception’, Music Perception, xiii (1995), 59–78
J. Roeder: ‘A Calculus of Accent’, JMT, xxxix (1995), 1–46
W. Rothstein: ‘Beethoven with and without Kunstgepränge: Metrical Ambiguity Reconsidered’, Beethoven Forum, iv, ed. C. Reynolds, L. Lockwood and J. Webster (Lincoln, NE, 1995), 165–93
C. Willner: ‘More on Handel and the Hemiola: Overlapping Hemiolas’, Music Theory Online, ii/3 (1996) 〈www.smt.ucsb.edu/mto>
C. Hasty: Meter as Rhythm (Oxford, 1997)
M. Yako: ‘The Hierarchical Structure of Time and Meter’, Computer Music Journal, xxi (1997), 47–57
A. Halm: ‘Rhythmik und Vortragsdynamik’, Von Grenzen und Ländern der Musik: gesammelte Aufsätze (Munich, 1916)
P. Farnsworth, H. Block and W. Waterman: ‘Absolute Tempo’, Journal of General Psychology, x (1934), 230–33
W. Gerstenberg: Die Zeitmasse und ihre Ordnungen in Bachs Musik (Einbeck, 1952)
I. Herrmann-Bengen: Tempobezeichnungen: Ursprung, Wandel im 17. und 18. Jahrhundert (Tutzing, 1959)
E. Barthe: Takt und Tempo: Studien über Zusammenhänge (Hamburg, 1960)
F. Eibner: ‘The Dotted-Quaver-and-Semiquaver Figure with Triplet Accompaniment in the Works of Schubert’, MR, xxiii (1962), 281–4
I. Barbag-Drexler: ‘Tempo rubato’, Musikerziehung, xxv (1972), 159–62
K.-E. Behne: Der Einfluss des Tempos auf die Beurteilung von Musik (Cologne, 1972)
A. Gabrielsson: ‘Performance of Rhythmic Patterns’, Scandinavian Journal of Psychology, xv (1974), 63–72
M. Yeston: ‘Rubato and the Middleground’, JMT, xix (1975), 286–301
K.-E. Behne: ‘Zeitmasse: zur Psychologie des musikalischen Tempoempfindens’, Mf, xxix (1976), 155–64
D.-J. Povel: ‘Temporal Structure of Performed Music: Some Preliminary Observations’, Acta psychologica, xli (1977), 309–20
J. Sundberg and V. Verrillo: ‘On the Anatomy of the Ritard: a Study of Timing in Music’, Speech Transmission Laboratory Quarterly Progress and Status Report, ii–iii (1977), 44–57
W. Berry: ‘Rhythmic Accelerations in Beethoven’, JMT, xxii (1978), 177–236
M. Serafine: ‘Meter Conservation in Music’, Council for Research in Music Education Bulletin, lix (1979), 94–7
I. Bengtsson and A. Gabrielsson: ‘Methods for Analyzing Performance of Musical Rhythm’, Scandinavian Journal of Psychology, xxi (1980), 257–68
E. Clarke: ‘Timing in the Performance of Erik Satie's “Vexations”’, Acta psychologica, l (1982), 1–19
M. Clynes and J. Walker: ‘Neurobiologic Functions of Rhythm, Time, and Pulse in Music’, Music, Mind, and Brain, ed. M. Clynes (New York, 1982), 171–216
L. Shaffer: ‘Rhythm and Timing in Skill’, Psychological Review, lxxxix/2 (1982), 109–22
J.A. Sloboda: ‘The Communication of Musical Metre in Piano Performance’, Quarterly Journal of Experimental Psychology, xxxv (1983), 377–96
C. Beauvillain and P. Fraisse: ‘On the Temporal Control of Polyrhythmic Performance’, Music Perception, i (1983–4), 485–99
E. Clarke: ‘Structure and Expression in Rhythmic Performance’, Musical Structure and Cognition, ed. P. Howell, I. Cross and R. West (New York, 1985), 209–36
U. Kronman and J. Sundberg: ‘Is the Musical Ritard an Allusion to Physical Motion?’, Action and Perception in Rhythm and Music: Uppsala 1985, 57–68
L. Shaffer and N. Todd: ‘The Interpretive Component in Musical Performance’, ibid., 139–52
N. Todd: ‘A Model of Expressive Timing in Tonal Music’, Music Perception, iii (1985–6), 33–58
M. Clynes and J. Walker: ‘Music as Time's Measure’, Music Perception, iv (1986–7), 85–120
C. MacKenzie and others: ‘The Effect of Tonal Structure on Rhythm in Piano Performance’, Music Perception, iv (1986–7), 215–26
C. Palmer and C. Krumhansl: ‘Pitch and Temporal Contributions to Musical Phrase Perception: Effects of Harmony, Performance Timing, and Familiarity’, Perception and Psychophysics, xli (1987), 505–18
A. Gabrielsson: ‘Timing in Performance and its Relation to Music Experience’, Generative Processes in Music, ed. J. Sloboda (Oxford, 1988), 27–51
C. Palmer: Timing in Skilled Piano Performance (diss., Cornell U., 1988)
J. Talley: Minor Variation in Performance as Indicators of Musical Meter (diss., Ohio State U., 1989)
N. Todd: ‘Towards a Cognitive Theory of Expression: the Performance and Perception of Rubato’, CMR, iv (1989), 405–16
K. Grieshaber: Polymetric Performance by Musicians (diss., U. of Washington, 1990)
R. Kendall and E. Carterette: ‘The Communication of Musical Expression’, Music Perception, viii (1990–91), 129–64
J. Sundberg, A. Friberg and L. Frydén: ‘Threshold and Performance Quantities of Rules for Music Performance’, Music Perception, ix (1991–2), 71–92
B. Repp: ‘Diversity and Commonality in Music Performance: an Analysis of Timing Microstructure in Schumann's “Träumerei”’, JASA, xcii (1992), 2546–68
E. Clarke: ‘Imitating and Evaluating Real and Transformed Musical Performances’, Music Perception, x (1992–3), 317–41
J. Feldman, D. Epstein and W. Richards: ‘Force Dynamics of Tempo Change in Music’, Music Perception, x (1992–3), 185–204
J. Geringer, C. Madsen and R. Duke: ‘Perception of Beat-Note Change in Modulating Tempos’, Bulletin of the Council for Research in Music Education, cxix (1994), 49–57
G. Hudson: Stolen Time: the History of Tempo Rubato (Oxford, 1994)
D.E. Rowland: ‘Chopin's Tempo Rubato in Context’, Chopin Studies, ii, ed. J. Rink and J. Samson (Cambridge, 1994), 199–213
D. Epstein: Shaping Time: Music, the Brain, and Performance (New York, 1995)
N. Todd: ‘The Kinematics of Musical Expression’, JASA, xcvi (1995), 1940–50
B. Repp: ‘The Detectability of Local Deviations from a Typical Expressive Timing Pattern’, Music Perception, xv (1997–8), 265–89
W. James: The Principles of Psychology (1890/R)
E. Meumann: ‘Untersuchungen zur Psychologie und Ästhetik des Rhythmus’, Philosophische Studien, x (1894), 249–322, 393–430
R. Stetson: ‘A Motor Theory of Rhythm and Discrete Sensation’, Psychological Review, xii (1905), 250–70, 293–350
K. Koffka: ‘Experimentale-Untersuchungen zur Lehre vom Rhythmus’, Zeitschrift für Psychologie, no.52 (1909), 1–109
H. Woodrow: ‘A Quantitative Study of Rhythm’, Archives of Psychology, xiv (1909), 1–66
M. Wertheimer: ‘Experimentelle Studien über das Sehen von Bewegung’, Zeitschrift für Psychologie, no.61 (1912), 161–265
E. Isaacs: ‘The Nature of the Rhythmic Experience’, Psychological Review, xxvii (1920), 270–99
J. Mainwaring: ‘Kinaesthetic Factors in the Recall of Music Experience’, British Journal of Psychology, xxiii (1933), 284–307
J. Mursell: The Psychology of Music (New York, 1937)
C. Seashore: Psychology of Music (New York, 1938)
K. Lashley: ‘The Problem of Serial Order in Behavior’, Cerebral Mechanisms in Behaviour: the Hixon Symposium, ed. L. Jeffress (New York, 1951), 112–36
P. Fraisse: Les structures rythmiques (Leuven, 1956)
L.B. Meyer: Emotion and Meaning in Music (Chicago, 1956)
R. Francès: La perception de la musique (Paris, 1958)
I. Hirsh: ‘Auditory Perception of Temporal Order’, JASA, xxxi (1959), 759–67
P. Fraisse: The Psychology of Time, trans. J. Leith (New York, 1963)
F. Matsuda: ‘Development of Time Estimation: Effects of Frequency of Sounds Given during Standard Time’, Japanese Journal of Psychology, xxxvi (1966), 285–94
H. de La Motte-Haber: Ein Beitrag zur Klassifikation musikalischer Rhythmen: experimental-psychologische Untersuchungen (Cologne, 1968)
R.E. Ornstein: On the Experience of Time (Harmondsworth, 1969)
P. Divenyi: The Rhythmic Perception of Micro-Melodies: Detectability by Human Observers of a Time Increment between Sinusoidal Pulses of Two Different, Successive Frequencies (diss., U. of Washington, 1970)
J. Martin: ‘Rhythmic (Hierarchical) versus Serial Structure in Speech and Other Behavior’, Psychological Review, lxxix (1972), 487–509
W. Dowling: ‘Rhythmic Groups and Subjective Chunks in Memory for Melodies’, Perception and Psychophysics, xiv (1973), 37–40
P. Vos: ‘Pattern Perception in the Measurement of Sound with Metrical-Organized Time Structures’, Nederlands tijdschrift voor de psychologie en haar grensgebieden, xxviii (1974), 565–80
D. Getty: ‘Discrimination of Short Temporal Intervals: a Comparison of Two Models’, Perception and Psychophysics, xviii (1975), 1–8
L. Van Noorden: Temporal Coherence in the Perception of Tone Sequences (diss., U. of Eindhoven, 1975)
L. Allan: ‘Is There a Constant Minimum Perceptual Duration?’, Quarterly Journal of Experimental Psychology, xxviii (1976), 71–6
E. Gordon: Tonal and Rhythm Patterns: an Objective Analysis (Albany, NY, 1976)
M. Jones: ‘Time, our Lost Dimension: Toward a New Theory of Perception, Attention, and Memory’, Psychological Review, lxxxiii (1976), 323–55
J. Sundberg and B. Lindblom: ‘Generative Theories in Language and Music Descriptions’, Cognition, iv (1976), 99–122
M. Steedman: ‘The Perception of Musical Rhythm and Metre’, Perception, vi (1977), 555–71
I. Bengtsson, A. Gabrielsson and B. Gabrielsson: ‘A Computer Program for Analysis of Rhythmic Performance’, STMf, xl (1978), 15–24
P. Fraisse: ‘Time and Rhythm Perception’, Handbook of Perception, viii, ed. E.C. Carterette and M.P. Friedman (New York, 1978)
L. Allan: ‘The Perception of Time’, Perception and Psychophysics, xxvi (1979), 340–54
J. Tenney and L. Polansky: ‘Temporal Gestalt Perception in Music’, JMT, xxiv (1980), 205–41
S. Handel and J. Oshinsky: ‘The Meter of Syncopated Auditory Polyrhythms’, Perception and Psychophysics, xxx (1981), 1–9
M. Jones, G. Kidd and R. Wetzel: ‘Evidence for Rhythmic Attention’, Journal of Experimental Psychology, vii (1981), 1059–73
D.-J. Povel: ‘Internal Representation of Simple Temporal Patterns’, Journal of Experimental Psychology, vii (1981), 3–18
R. Wood: The Perceptual Processing of Rhythmic Auditory Pattern Temporal Order (diss., U. of Michigan, 1981)
D. Deutsch: ‘Grouping Mechanisms in Music’, The Psychology of Music (New York, 1982), 99–134
D. Deutsch: ‘Organizational Processes in Music’, Music, Mind, and Brain, ed. M. Clynes (New York, 1982), 119–36
P. Fraisse: ‘Rhythm and Tempo’, The Psychology of Music, ed. D. Deutsch (New York, 1982), 149–80
A. Halpern and C. Darwin: ‘Duration Discrimination in a Series of Rhythmic Events’, Perception and Psychophysics, xxxi (1982), 86–9
M. Jones, M. Boltz and G. Kidd: ‘Controlled Attending as a Function of Melodic and Temporal Context’, Perception and Psychophysics, xxxii (1982), 211–18
H. Longuet-Higgins and C. Lee: ‘The Perception of Musical Rhythms’, Perception, xi (1982), 115–28
A. Gabrielsson, I. Bengtsson and B. Gabrielsson: ‘Performance of Musical Rhythm in 3/4 and 6/8 Meter’, Scandinavian Journal of Psychology, xxiv (1983), 193–213
J.A. Sloboda: ‘The Communication of Musical Metre in Piano Performance’, Quarterly Journal of Experimental Psychology, xxxvA (1983), 377–96
S. Handel: ‘Using Polyrhythms to Study Rhythm’, Music Perception, i (1983–4), 465–84
Action and Perception in Rhythm and Music: Uppsala 1985 [incl. P. Fraisse: ‘A Historical Approach to Rhythm as Perception’, 7–18; A. Friberg, J. Sundberg and L. Frydén: ‘How to Terminate a Phrase: an Analysis-by-Synthesis Experiment on a Perceptual Aspect of Music Performance’, 201–33]
P. Essens and D.-J. Povel: ‘Metrical and Nonmetrical Representations of Temporal Patterns’, Perception and Psychophysics, xxxvii (1985), 1–7
S. Klapp and others: ‘On Marching to Two Different Drummers: Perceptual Aspects of the Difficulties’, Journal of Experimental Psychology, xi (1985), 814–27
A. Gabrielsson: ‘Interplay between Analysis and Synthesis in Studies of Music Performance and Music Experience’, Music Perception, iii (1985–6), 59–86
J. Bharucha and J. Pryor: ‘Distrupting the Isochrony Underlying Rhythm: an Asymmetry in Discrimination’, Perception and Psychophysics, xl (1986), 137–41
P. Essens: ‘Hierarchical Organization of Temporal Patterns’, Perception and Psychophysics, xl (1986), 69–73
M. Jones: ‘Attentional Rhythmicity in Human Perception’, Rhythm in Psychological, Linguistic, and Musical Processes, ed. J.R. Evans and M. Clynes (Springfield, IL, 1986)
I. Deliège: ‘Grouping Conditions in Listening to Music: an Approach to Lerdahl and Jackendoff's Grouping Preference Rules’, Music Perception, iv (1986–7), 325–60
W. Hutchinson and L. Knopoff: ‘The Clustering of Temporal Elements in Melody’, Music Perception, iv (1986–7), 281–303
E. Clarke: ‘Levels of Structure in the Organization of Musical Time’, CMR, ii (1987), 211–38
W. Dowling, K. Lung and S. Herrbold: ‘Aiming Attention in Pitch and Time in the Perception of Interleaved Melodies’, Perception and Psychophysics, xli (1987), 642–56
M. Jones: ‘Dynamic Pattern Structure in Music: Recent Theory and Research’, Perception and Psychophysics, xli (1987), 621–34
Y. Nakajima: ‘A Model of Empty Duration Perception’, Perception, xvi (1987), 485–520
B. Rosner: ‘Music Perception, Music Theory, and Psychology’, Explorations in Music, the Arts, and Ideas: Essays in Honor of Leonard B. Meyer, ed. E. Narmour and R. Solie (Stuyvesant, NY, 1988), 141–75
A. Halpern: ‘Perceived and Imagined Tempos of Familiar Songs’, Music Perception, vi (1988–9), 193–202
D. Rosenthal: ‘A Model for the Process of Listening to Simple Rhythms’, Music Perception, vi (1988–9), 315–28
E. Clarke: ‘The Perception of Expressive Timing in Music’, Psychological Research, li (1989), 2–9
P. Desain and H. Honing: ‘The Quantization of Musical Time: a Connectionist Approach’, Computer Music Journal, xiii (1989), 56–66
R. Duke: ‘Musicians' Perception of Beat in Monotonic Stimuli’, JRME, xxxvii (1989), 61–71
R.O. Gjerdingen: ‘Meter as a Mode of Attending: a Network Simulation of Attentional Rhythmicity in Music’, Integral, iii (1989), 67–91
S. Handel: Listening: an Introduction to the Perception of Auditory Events (Cambridge, 1989)
M. Jones and M. Boltz: ‘Dynamic Attending and Responses to Time’, Psychological Review, xcvi (1989), 459–91
H.-H. Schulze: ‘Categorical Perception of Rhythmic Patterns’, Psychological Research, li (1989), 10–15
E. Clarke and C. Krumhansl: ‘Perceiving Musical Time’, Music Perception, vii (1989–90), 213–52
R.O. Gjerdingen: ‘Categorization of Musical Patterns by Self-Organizing Neuronlike Networks’, Music Perception, vii (1989–90), 339–69
E. Bigand: ‘Abstraction of Two Forms of Underlying Structure in a Tonal Melody’, Psychology of Music, xviii (1990), 45–59
A. Bregman: Auditory Scene Analysis: the Perceptual Organization of Sound (Cambridge, MA, 1990)
I. Hirsh and others: ‘Studies in Auditory Timing, 1: Simple Patterns’, Perception and Psychophysics, xlvii (1990), 215–26
M. Jones: ‘Learning and the Development of Expectancies: an Interactionist Approach’, Psychomusicology, ix (1990), 193–228
C. Palmer and C. Krumhansl: ‘Mental Representations for Musical Meter’, Journal of Experimental Psychology, xvi (1990), 728–41
M. Treisman and others: ‘The Internal Clock: Evidence for a Temporal Oscillator Underlying Time Perception, with Some Estimates of its Characteristic Frequency’, Perception, xix (1990), 705–43
Y. Nakajima, G. Ten Hoopen and R. Van Der Wilk: ‘A New Illusion of Time Perception’, Music Perception, viii (1990–91), 431–48
P. Desain and H. Honing: ‘Tempo Curves Considered Harmful’, Computer Music Conference: Montreal 1991, 143–9
P. Johnson-Laird: ‘Rhythm and Meter: a Theory at the Computational Level’, Psychomusicology, x/2 (1991), 88–106
C. Lee: ‘The Perception of Metrical Structure: Experimental Evidence and a Model’, Representing Musical Structure, ed. P. Howell, R. West and I. Cross (New York, 1991), 59–127
P. Desain: ‘A (De)Composable Theory of Rhythm Perception’, Music Perception, ix (1991–2), 439–54
D. Butler: The Musician's Guide to Perception and Cognition (New York, 1992)
C. Collyer and others: ‘Categorical Time Production: Evidence for Discrete Timing in Motor Control’, Perception and Psychophysics, li (1992), 134–44
P. Desain and H. Honing: ‘Time Functions Function Best as Functions of Multiple Times’, Computer Music Journal, xvi (1992), 17–34
M. Jones: ‘Attending to Musical Events’, Cognitive Bases of Musical Communication: Columbus, OH, 1990, ed. M. Jones and S. Holleran (Washington, 1992), 91–110
C. Linster: ‘On Analyzing and Representing Musical Rhythm’, Understanding Music with AI: Perspectives on Music Cognition, ed. M. Balaban, K. Ebcioglu and O.E. Laske (Cambridge, MA, 1992), 414–27
B. Miller, D. Scarborough and J. Jones: ‘On the Perception of Meter’, ibid., 428–47
C. Palmer and M.H. Kelly: ‘Linguistic Prosody and Musical Meter in Song’, Journal of Memory and Language, xxxi (1992), 525–42
D. Rosenthal: Machine Rhythm: Computer Emulation of Human Rhythm (diss., MIT, 1992)
C. Drake and C. Palmer: ‘Accent Structures in Music Performance’, Music Perception, x (1992–3), 343–78
R. Gjerdingen: ‘“Smooth” Rhythms as Probes of Entrainment’, Music Perception, x (1992–3), 503–8
M. Boltz: ‘Time Estimation and Expectancies’, Memory and Cognition, xxi (1993), 853–63
C. Brower: ‘Memory and the Perception of Rhythm’, Music Theory Spectrum, xv (1993), 19–35
L. Dawe and others: ‘Harmonic Accents in Inference of Metrical Structure and Perception of Rhythm Patterns’, Perception and Psychophysics, liv (1993), 194–207
C. Drake: ‘Perceptual and Performed Accents in Musical Sequences’, Bulletin of the Psychonomic Society, xxxi (1993), 107–10
M. Jones and W. Yee: ‘Attending to Auditory Events: the Role of Temporal Organization’, Thinking in Sound: the Cognitive Psychology of Human Audition, ed. S. McAdams and E. Bigand (Oxford, 1993), 69–112
B. Miller: ‘Time Perception in Musical Meter Perception’, Psychomusicology, xii (1993), 124–53
I. Peretz and R. Kolinsky: ‘Boundaries of Separability between Melody and Rhythm in Music Discrimination: a Neuropsychological Perspective’, Quarterly Journal of Experimental Psychology Section A: Human Experimental Psychology, xlvi/2 (1993), 301–25
W. Windsor: ‘Dynamic Accents and the Categorical Perception of Metre’, Psychology of Music, xxi (1993), 127–40
R.O. Gjerdingen: ‘Apparent Motion in Music?’, Music Perception, xi (1993–4), 335–70
R. Parncutt: ‘A Perceptual Model of Pulse Salience and Metrical Accent in Musical Rhythms’, Music Perception, xi (1993–4), 409–64
R. Duke: ‘When Tempo Changes Rhythm: the Effect of Tempo on Nonmusicians' Perception of Rhythm’, JRME, xlii (1994), 27–35
L. Shaffer and N.P.M. Todd: ‘The Interpretive Component in Musical Performance’, Musical Perceptions, ed. R. Aiello (New York, 1994), 258–70
W. Yee and others: ‘Sensitivity to Event Timing in Regular and Irregular Sequences: Influences of Musical Skill’, Perception and Psychophysics, lvi (1994), 461–71
N. Dibben: ‘The Cognitive Reality of Hierarchic Structure in Tonal and Atonal Music’, Music Perception, xii (1994–5), 1–25
E. Gallun and D. Reisberg: ‘On the Perception of Interleaved Melodies’, Music Perception, xii (1994–5), 387–398
M. Boltz: ‘The Generation of Temporal and Melodic Expectancies during Musical Listening’, Perception and Psychophysics, liii (1995), 585–600
G. Collier and C. Wright: ‘Temporal Rescaling of Simple and Complex Ratios in Rhythmic Tapping’, Journal of Experimental Psychology, xxi (1995), 602–27
R. Ivry and R. Hazeltine: ‘Perception and Production of Temporal Intervals across a Range of Durations: Evidence for a Common Timing Mechanism’, Journal of Experimental Psychology, xxi (1995), 3–18
M. Jones and others: ‘Test of Attentional Flexibility in Listening to Polyrhythmic Patterns’, Journal of Experimental Psychology, xxi (1995), 293–307
J. Roederer: The Physics and Psychophysics of Music: an Introduction (New York, 3/1995)
M. Royal: The Perception of Rhythm and Tempo Modulation in Music (diss., U. of Western Ontario, 1995)
B. Repp: ‘Quantitative Effects of Global Tempo on Expressive Timing in Music Performance: Some Perceptual Evidence’, Music Perception, xiii (1995–6), 39–57
T. Ryan: Grouping Strategy in Rhythmic Perception: a Test of the Perceptual Salience of Lerdahl and Jackendoff's Grouping Preference Rules (diss., Ohio State U., 1996)
C. Palmer: ‘On the Assignment of Structure in Music Performance’, Music Perception, xiv (1996–7), 23–56
M. Jones and W. Yee: ‘Sensitivity to Time Change: the Role of Context and Skill’, Journal of Experimental Psychology, xxiii (1997), 693–709
R. Waterman: ‘“Hot” Rhythm in Negro Music’, JAMS, i (1948), 24–37
C. Brăiloiu: ‘Le rythme aksak’, RdM, xxx (1951), 71–108; ed. G. Rouget in Problèmes d'ethnomusicologie (Paris, 1959; Eng. trans., 1984), 133–67
C. Brăiloiu: ‘Le giusto syllabique’, Polyphonie, ii (1952), 26–57; ed. G. Rouget in Problèmes d'ethnomusicologie (Paris, 1959; Eng. trans., 1984), 168–205
A.D. Motsev: ‘Rhythm and Time in Bulgarian Folk Music’, JIFMC, iv (1952), 83
E. Harich-Schneider: The Rhythmical Patterns in Gagaku and Bugaku (Leiden, 1954)
J. Blacking: ‘Some Notes on a Theory of African Rhythm Advanced by Erich von Hornbostel (Suggested Contrast between African and European Concepts)’, AfM, i (1955), 12–20
A.M. Jones: African Rhythm (London, 1955)
A. Merriam: ‘Characteristics of African Music’, JIFMC, xi (1959), 13–19
C. Gregoire: Ägyptische Rhythmik: Rhythmen und Rhythmusinstrumente im heutigen Ägypten (Strasbourg, 1960)
J.H.K. Nketia: Drumming in Akan Communities of Ghana (Edinburgh, 1963)
J. Becker: ‘Percussive Patterns in the Music of Mainland Southeast Asia’, EthM, xii (1968), 173–91
H. Koshiba: ‘Rhythm in nō music’, Nihon ongaku to sono shūhen: Kikkawa Eishi sensei kanneki kinen roubunshū [On Japanese music: articles to celebrate the 60th birthday of Eishi Kikkawa], ed. A. Hoshi, F. Koizumi and O. Yamaguchi (Tokyo, 1973), 179–208
J.H.K. Nketia: The Music of Africa (New York, 1974)
G. Tsuge: Avaz: a Study of the Rhythmic Aspects in Classical Iranian Music (diss., Wesleyan U., 1974)
N. Linh: Le rythme dans la musique vietnamienne (diss., U. of Paris, 1975)
L.E. Ekwueme: ‘Structural Levels of Rhythm and Form in African Music, with Particular Reference to the West Coast’, AfM, v (1976–7), 27–35
N. Ghosh: Fundamentals of Raga and Tala, with a New System of Notation (Bombay, 1978)
J. Chernoff: African Rhythm and African Sensibility: Aesthetics and Social Action in African Musical Idioms (Chicago, 1979)
G. List: ‘African Influence in the Rhythmic and Metric Organization of Colombian Costeno Folksong and Folk Music’, LAMR, i (1980), 16–17
H. Lee: ‘Triple Meter and its Prevalence in Korean Music’, Music East and West: Essays in Honor of Walter Kaufmann, ed. T. Noblit (New York, 1981), 101–10
A. Merriam: ‘African Musical Rhythm and Concepts of Time-Reckoning’, ibid., 123–41
D. Locke: ‘Principles of Offbeat Timing and Cross-Rhythm in Southern Eve Dance Drumming’, EthM, xxvi (1982), 217–46
J. Pressing: ‘Rhythmic Design in the Support Drums of Agbadza’, AfM, vi/3 (1983), 4–15
R. Stone: ‘In Search of Time in African Music’, Music Theory Spectrum, vii (1985), 139–48
J.P. Blom and T. Kvifte: ‘On the Problem of Inferential Ambivalence in Musical Meter’, EthM, xxx (1986), 491–517
J. Maceda: ‘A Concept of Time in a Music of Southeast Asia (a Preliminary Account)’, EthM, xxx (1986), 11–53
L. Rowell: ‘The Ancient Tala System: a Comparative Approach’, Journal of the Music Academy of Madras, lvii (1986), 83–99
K. Agawu: ‘The Rhythmic Structure of West African Music’, JM, v (1987), 400–18
D. Avorgbedor: ‘The Construction and Manipulation of Temporal Structures in Yeve Cult Music’, AfM, vi/4 (1987), 4–18
O. Elschek: ‘Rhythmik und Metrik in traditionellen Musikkulturen’, Musicologica slovaca, xvi (1990)
C. Kaden: ‘Haltetone als metro-rhythmisches Organisationsprinzip’, Musicologica slovaca, xvi (1990), 269–86
S. Arom: African Polyphony and Polyrhythm (Cambridge, 1991)
V.K. Agawu: ‘Representing African Music’, Critical Inquiry, xviii (1991–2), 245–66
J. Cler: ‘Aksak Theory’, RdM, lxxx (1994), 181–210
V.K. Agawu: African Rhythm: a Northern Ewe Perspective (Cambridge, 1995)
V.K. Agawu: ‘The Invention of “African Rhythm”’, JAMS, xlviii (1995), 380–95
H.L. Bergson: Essai sur les données immédiates de la conscience (Paris, 1889/R)
H.L. Bergson: Matière et mémoire (Paris, 1896, 5/1908; Eng. trans., 1911)
H.L. Bergson: Durée et simultanéité (Paris, 1922)
C. Koechlin: ‘Le temps et la musique’, ReM, vii/7–8 (1926), 45–62
A.N. Whitehead: Process and Reality: and Essay in Cosmology (New York, 1929)
H. Mersmann: ‘Zeit und Musik’, Zeitschrift für Ästhetik und allgemeine Kunstwissenschaft, xxv (1931), 216
R. Harding: Origins of Musical Time and Expression (London, 1938)
P. Souvtchinsky: ‘La notion du temps et la musique’, ReM, nos.188–91 (1939), 70–80, 309–20
G. Brelet: Le temps musical (Paris, 1949)
S. Langer: Feeling and Form (New York, 1953)
A. Briner: Der Wandel der Musik als Zeit-Kunst (Vienna, 1955)
E. Lendvai: Bartók stilusa (Budapest, 1955)
S. Langer, ed.: Reflections on Art (London, 1958)
W. Dürr: ‘Rhythm in Music: a Formal Scaffolding of Time’, The Voices of Time, ed. J.T. Fraser (New York, 1966), 180–200
C. Keil: ‘Motion and Feeling through Music’, Journal of Aesthetics and Art Criticism, xxiv (1966), 337–49
P. Carpenter: ‘The Musical Object’, CMc, no.5 (1967), 56–86
F. Martin: ‘The Power of Music and Whitehead's Theory of Perception’, Journal of Aesthetics and Art Criticism, xxv (1967), 313–22
E. Altwein: ‘Zeit und Musik’, SMz, cviii (1968), 305–13
Z. Lissa: ‘The Temporal Nature of a Musical Work’, Journal of Aesthetics and Art Criticism, xxvi (1968), 529–38
M. Rotharmel: Der musikalische Zeitbegriff seit Moritz Hauptmann (Regensburg, 1968)
T. Hori: ‘Ongaku no rizumo–jikanron–teki kanten kara’ [Musical rhythm: from the point of view of time], Ongaku-gaku, xv (1969), 66–76
A. Pike: A Phenomenological Analysis of Musical Experience and Other Related Essays (New York, 1970)
W. Seidel: ‘Descartes Bemerkungen zur musikalischen Zeit’, AMw, xxvii (1970), 287–303
M. Čapek: Bergson and Modern Physics (Dordrecht, 1971)
E. Cone: ‘Music: a View from Delft’, Perspectives on Contemporary Music Theory, ed. B. Boretz and E.T. Cone (New York, 1972), 57–71
W. Dalton: The Fulfillment of Time: a Langerian/Whiteheadian Aesthetic of Music Performance (diss., Clermont School of Theology, 1974)
E. Emery: Temps et musique (Lausanne, 1975)
G. Rochberg: ‘The Structure of Time in Music: Traditional and Contemporary Ramifications and Consequences’, The Study of Time, ii, ed. J.T. Fraser and N. Lawrence (New York, 1975), 136–49
T. Clifton: ‘The Poetics of Musical Silence’, MO, lxii (1976), 163–81
D. Ihde: Listening and Voice: a Phenomenology of Sound (Athens, OH, 1976)
R. Newell: ‘Four Tiers on the Foundation of Time’, IRASM, vii (1976), 147–73
M. Rogers: The Golden Section in Musical Time: Speculations on Temporal Proportion (diss., U. of Iowa, 1977)
M. Barela: ‘Motion in Musical Time and Rhythm’, College Music Symposium, xix (1979), 78–92
J. Perry-Camp: ‘Time and Temporal Proportion: the Golden Section Metaphor in Mozart, Music, and History’, JMR, iii (1979), 133–76
L. Rowell: ‘The Subconscious Language of Musical Time’, Music Theory Spectrum, i (1979), 96–106
F. Smith: The Experiencing of Musical Sound: Prelude to a Phenomenology of Music (New York, 1979)
R. Morgan: ‘Musical Time/Musical Space’, Critical Inquiry, vi (1979–80), 527–38
P. Alperson: ‘“Musical Time” and Music as an “Art of Time”’, Journal of Aesthetics and Art Criticism, xxxviii (1980), 407–17
M. Imberty: Les écritures du temps: sémantique psychologique de la musique (Paris, 1981)
J. Lochhead: The Temporal Structure of Recent Music: a Phenomenological Investigation (diss., SUNY, 1982)
T. Clifton: Music as Heard: a Study in Applied Phenomenology (New Haven, CT, 1983)
S. Levarie and E. Levy: Musical Morphology: a Discourse and a Dictionary (Kent, OH, 1983)
D. Greene: Consciousness and Temporality (New York, 1984)
G. Rochberg: ‘The Concepts of Musical Time and Space’, The Aesthetics of Survival (Ann Arbor, 1984), 78–136
H. de La Motte-Haber: ‘Tradition und Vergangenheit: über das Zeiterleben’, Österreichischer Musikrat Bulletin, i (1985), 3–11
D. Lewin: ‘Music Theory, Phenomenology, and Modes of Perception’, Music Perception, iii (1985–6), 327–92
J. Judkins: The Aesthetics of Musical Silence: Virtual Time, Virtual Space, and the Role of the Performer (diss., UCLA, 1987)
J. Kramer: The Time of Music (New York, 1988)
A. Chandra: On the Construction of the Passing of Time in Music (diss., U. of Illinois, 1989)
J. Lochhead: ‘The Metaphor of Musical Motion: is There an Alternative?’, Theory and Practice, xiv–xv (1989–90), 83–103
B. Barry: Musical Time: the Sense of Order (Stuyvesant, NY, 1990)
J. Kramer, ed.: ‘Time in Contemporary Musical Thought’, CMR, vi (1993)