major triad. Such a
definition is, in turn, further refined by larger musical contexts, and the
roles of rhythm, register, dynamics and timbre in tonal music are closely
related to, and interactive with, the definition of tonal functions.A term that may be used in three senses: first, to describe all music which is not tonal; second, to describe all music which is neither tonal nor serial; and third, to describe specifically the post-tonal and pre-12-note music of Berg, Webern and Schoenberg. (While serial music is, by the first definition, atonal, it differs in essential respects from other atonal music and is discussed in the articles Serialism and Twelve-note composition; it is, therefore, not considered here.)
1. Relations between tonality and atonality.
2. Differences between tonality and atonality.
3. The atonality of Schoenberg, Berg and Webern.
PAUL LANSKY, GEORGE PERLE (1–3, 5), DAVE HEADLAM (4, bibliography)
An
important aspect of tonality is the way in which pitches are contextually
defined so that each particular definition of a given pitch yields a different
tonal function. A G which is the root of a G major triad, for example, has a
different function or meaning from that of a G which is the 3rd of an E major triad. Such a
definition is, in turn, further refined by larger musical contexts, and the
roles of rhythm, register, dynamics and timbre in tonal music are closely
related to, and interactive with, the definition of tonal functions.
Atonality may be seen roughly to delimit two kinds of music: (1) That in which there is no such contextual definition with reference to triads, diatonic scales or keys, but in which there are, nonetheless, hierarchical distinctions among pitches. This category would include some of the works of Schoenberg, Stravinsky and Hindemith. The inadequacy of theories of tonality in dealing with this music lends support to such a classification. (2) That in which such hierarchical distinctions are not so explicit, though sometimes present. This includes some of the pre-serial music of Webern, Schoenberg and, to a lesser extent, Berg.
The usual attitudes concerning atonality and its development are vague and misleading. It is often said that tonality developed to a point of complexity where it was no longer possible to determine contextual definition as described, and tonal functions were therefore abandoned. This attitude has a basis in reality but is a simplification which obscures essential issues. Two compositions near either side of the imagined border between tonality and atonality, Liszt’s Sonetto del Petrarca no.104 from the second book of Années de pèlerinage, and Skryabin’s Prelude op.74 no.3, shed light on this question.
It
is not difficult to determine tonal contextual definition in the opening
measures of the Sonetto (ex.1). The F
dominant 7th chord at the downbeats of
bars 1, 4 and 5 serves as a dominant to the B dominant 7th in bar 5, which is
in turn the dominant of E in bar 7. In the opening bars of this composition,
however, the diminished 7th chord plays a fundamental role as a referential
collection through the use of different interpretations of that chord. The
chords at the upbeats to bars 1, 2, 3, 4 and 5, and at the fourth quaver beats
of bars 3 and 4, are all enharmonically equivalent forms of the initial
diminished 7th collection B, D, F, A, which is transformed into the dominant 7th chord
C, E, F, A on the downbeat of bar 1. In that bar the F octave moves to G as an
upper neighbour, at which point another diminished collection is implied: C, E, G, (B). The sequence is repeated at
successive minor 3rd transpositions until in bar 4 an octave transposition of
the F dominant 7th
chord of bar 1 is reached. All pitches in bars 1–4 are thus enharmonically
equivalent members of one of two diminished 7th collections. While it is useful
to observe that these measures prolong the dominant of the dominant of E major,
the actual method of prolongation is most easily understood in relation to the
enharmonically undefined diminished 7th collections 0, 3, 6, 9 and 1, 4, 7, 10
(with 0 denoting C or B,
1 denoting C or D, etc.). The absence of a
key signature further emphasizes the non-diatonic nature of the passage.
The
opening of Skryabin’s Prelude op.74 no.3 provides an interesting
counter-example (ex.2). The music is not tonal in
the senses described above or in the sense of the Liszt composition. It is not
clear that any note is defined as a member of a major or minor triad, or that
the passage is using notes of some major or minor scale. There is a ‘dominant
7th chord’ embedded in bar 2, but this does not seem to function as a dominant
of D major or minor. On the other hand a special aspect of this passage is that
all notes except G in
bar 1 and D in bar 3 belong to one of the diminished 7th collections A, C, E, G and B, D, F, A; and Skryabin’s spelling is consistent with this
view. The ‘dominant 7th chord’ in bar 2 is thus understood as a conjunction of
members of these two collections. In bar 3 the tritone transposition of the right
hand of bar 1, against the untransposed bass, results in the appearance of the
same collection as in bar 1 since the diminished 7th collection is invariant
under transposition by a tritone, The G–A succession in the middle register in bars 2–3 also
emphasizes the unfolding of a diminished 7th collection.
In response to the above attitude concerning the development of atonality, it would seem safe to say, rather, that tonality developed new ideas, which then lost some of their association with older concepts, and in doing so gained more independent status as compositional determinants. The diminished 7th chord in the music of Mozart, for example, most often acts as a tonicizing agent, with the two tritones resolving in contrary motion to a major or minor triad, but in the Liszt piece this is not so clearly the case, in that the chord seems to have some significance as a referential collection, and in the Skryabin it certainly functions in a completely different way.
In as much as notation reflects compositional thinking, it is interesting to observe the expanded denoting of key signatures in the late 19th and early 20th centuries as a kind of musical barometer. The point of a key signature in the music of Debussy, for example, is often only to delimit a pitch-class collection – usually the whole or part of a diatonic scale – rather than to prescribe a diatonic scale with the implied functional associations of tonic and dominant triads, consonance and dissonance, and so on, as in the notation and music of Liszt. On the other hand, the key signature of four sharps in Schoenberg’s Chamber Symphony op.9 serves more to indicate that an E major triad will function in some hierarchically significant way than to delimit a scale. The first pages of the composition are, in fact, so full of symmetrical collections, such as the whole-tone scale and the augmented triad, that the key signature serves virtually no practical purpose. In the fourth movement of Schoenberg’s Second Quartet op.10 the convention of a key signature is abandoned. Schoenberg commented upon this work as follows (as quoted by W. Reich in Schoenberg, London, 1971, p.31):
there are many sections in which the individual parts proceed regardless of whether or not their meeting results in codified harmonies …. The key is presented distinctly at all the main dividing points of the formal organization. Yet the overwhelming multitude of dissonances cannot be balanced any longer by occasional returns to such triads as represent a key.
The concept of atonality thus evolved as various components of tonality lost the high degree of interdependence they had formerly possessed.
An important aspect of late 19th-century music lies in a set of relatively abstract ideas about what music is and can be: a referential sonority (the triad) as the basis of a musical language; a motif as a compositional tool; the progress and unfolding of a musical composition as something defined by the transformation and development of motivic, contrapuntal and harmonic ideas; the concept of closure; significant relations between discrete parts of a musical composition; and the hierarchic superiority of certain specific pitches or configurations of pitches in a given composition. The first composers whose music might be defined as atonal were trained in the traditions of 19th-century tonality, and their music reveals, in one way or another, the profound influence of these concepts, as may be exemplified by the opening of the second of Schoenberg’s Five Orchestral Pieces op.16 (ex.3 is taken from Webern’s two-piano reduction).
A
succession of simultaneities between the two right hands unfolds transpositions
and inversions (of interval content) of the same referential sonority: in bar
1, (A, D, G), (F, C,
G); in bar 2, (A, D, G), (G, C, G), (E, B, F). The significance of the D–A
dyad is emphasized by its role in the first movement, where the trichord D, A,
C is sustained as a
pedal for most of the movement, and by the octave doubling in bar 1 of ex.3 and
the retention of the D–A dyad for the first three bars. An important motivic
idea here is a three-note melodic cell consisting of some kind of 2nd and some
kind of 3rd. (In the opening of the first movement the cellos play the line (E,
F, A, G, A, C) which consists of several
interlocking versions of this cell.) The first three bars form a phrase unit
defined by the new rhythmic and registral placement of the descending minor 3rd
(G–F in bar 1; A–F in bar 3), and the rest
on the first beat of bar 4. The concept of a musical language as inferred from
tonality thus extends deeply into atonality and forms a significant basis for
the development of new ideas.
Although an attempt has been made to indicate the ways in which tonality developed into atonality and the similarities between the two, there are also significant differences. As has been noted, one of the remarkable aspects of tonality is the high degree of interdependence between the various dimensions of a composition, such as pitch, rhythm, dynamics, timbre and form. In atonality the functional relations between these dimensions are not clearly defined. The concept of a suspension in tonality, for example, embodies a conjunction of rhythmic and harmonic ideas, but the body of atonal works offers no similar operation as a general procedure. Comparisons of this sort have given rise to a second prevalent attitude concerning atonality: that its processes do not extend beyond the boundaries of a given composition. Again, this attitude is not entirely without basis but is highly oversimplified. As understanding of tonality is aided by the existence of a relatively highly developed theory, while no such assistance exists for atonality, the former is perceived as a more highly unified musical language than the latter. Atonal works do, however, have properties in common, but the manifestations of these properties are very different. Examples may be taken from two compositions in which, as in exx.1 and 2, the diminished 7th collection has some structural significance: the first movement of Bartók’s Music for Strings, Percussion and Celesta, and the opening of Varèse’s Density 21·5 for solo flute.
Ex.4 is the theme of the ‘fugue’ that opens
the Bartók work. The voices of the fugue make their entries at successive
perfect 5ths alternately above and below the original entry until, in bars 26
and 27, F and C are
reached, a major 13th above and below the original entry. The F and C are members of the same
diminished 7th collection as the initial A. They are doubled at the octave to
emphasize their structural significance, and they initiate a more complex
process of development which culminates in bar 56 where an E (the pitch class at which the two
diverging cycles of 5ths meet, and the remaining member of the diminished 7th
collection A, C, E, F) is reached. The linear
structure of the theme is relevant to the large-scale structure of the
movement. The first two phrases span A–E, an interval of the diminished 7th collection; the
third and fourth phrases span B–E and B–E, respectively. Thus a tritone, an interval which
figures in the large-scale structure, is outlined by the first and second
phrases, and also by the third and fourth phrases together. The span of the
entire theme is a perfect 5th, anticipating the second statement on E. At bar
65, after E is stated
in several octaves, the literal inversion of the theme is introduced, and at
the end of the movement (ex.5) a simultaneous statement of
the second phrase of the theme and of its inversion, both beginning on A,
telescopes structural aspects of the movement in the unison A and octave E, and in the statement of
all 12 pitch classes, a totality implied by the succession of fugal
transpositional levels, and created by any two adjacent fugal entries.
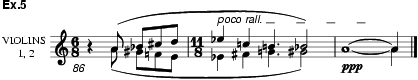
Ex.6 contains the first large phrase of
Varèse’s Density 21·5. The number 0, 1, or 2, inserted below each note,
shows the diminished 7th collection to which that note belongs: 0 denotes the
collection on C, 1 that on C and 2 that on D. Except for the Fs in bars 1 and 3,
all notes in bars 1–10 belong to the 0 and 1 collections. These bars seem, in
addition, to prolong the 1 collection since the 0 collection appears less
frequently and with less rhythmic emphasis. The opening F–E–F motif is special in that it
contains one member of each collection. Bar 9 represents an important
structural point: it is the loudest moment in the piece so far; the initial
rhythmic figure returns, but with new and more emphatic articulation; an octave
has been spanned from the lowest note so far and, since the 1 collection is now
represented on the first semiquaver of this figure, a kind of ‘modulation’
occurs. The repetition of D–C in bars 9 and 10 delays the arrival of D
(dynamically emphasized) until the downbeat of bar 11, thus prolonging a
transposition of the initial motif. In bars 11–13 there are successive
prolongations of the 2 and 0 collections, and a final return to the initial 1
collection. The B–E
dyad in bars 13–14 contains the remaining members of the 1 collection as it
appeared in its first salient statement in bar 2.
In both the Bartók and the Varèse a governing structural principle is the symmetrical partition of the octave through the diminished 7th collection. But the compositional procedures are very different and the respective results could hardly be more dissimilar.
Many of the atonal compositions of Berg, Webern and Schoenberg use procedures and concepts such as those discussed in relation to Schoenberg’s op.16 no.2. Just as tonality yielded concepts which were reinterpreted for use in atonality, so the interactions between the various aspects of the atonality of Berg, Webern and Schoenberg yielded new concepts which eventually became relevant to serialism. A fundamental development was the elimination of hierarchical pitch-class distinctions, typified in tonality by entities such as the major scale. This led to the use of all 12 pitch classes within smaller time spans. Webern’s Bagatelles for string quartet, for example, emphasize the unfolding of 12-note collections through a reduction of pitch and pitch-class repetition, and by very careful and precise attention to the articulation and orchestration of individual pitch classes (ex.7). The extreme brevity of each of the Bagatelles is a consequence of this approach.
The sense of octave relations as manifested in tonality undergoes a radical transformation in a composition such as the Bagatelles. Clearly defined octave relations would shift the focus away from an unfolding of the 12 pitch classes. This thinking strongly influenced the development of the 12-note system where the collection of 12 pitch classes plays a fundamental role. (The meaning of an octave relation in this music differs profoundly from that in the Bartók and Varèse examples quoted above. In the latter compositions the octave has significance as a boundary, framing its symmetrical divisions – the whole-tone scale, the diminished 7th collection, the augmented triad, the tritone and the cycles of 5ths and semitones – and octave intervals may thus signify the culmination of a process of development or a common feature of different subdivisions.) In this sense one motivic idea of the Bagatelles is a tendency towards the unfolding of 12-note collections. In general the concept of a motif in this music merges into a much broader background encompassing the rhythmic and instrumental textures.
The atonal works of Berg, Webern and Schoenberg employ a wide variety of procedures and techniques for securing musical coherence. It is only necessary to compare Schoenberg’s Erwartung with his Six Little Piano Pieces op.19, for example, to see, on the one hand, a large-scale unfolding of complex and varied pitch relations, and on the other, a small, detailed and precise expression of specific and simple musical ideas. The evolution to the 12-note system and serialism was guided mainly by a tendency to subdue traditional hierarchical pitch distinctions and to emphasize the use of ordered, or partially ordered, collections of pitch classes, or motifs, to generate chords and lines. Eventually the former tendency, in its encouragement of the use of 12-note collections, merged with the latter to become Schoenberg’s 12-note system.
In the latter half of the 20th century, three theories of organizational structures in atonal music emerged and became influential in musicians' perceptions and understanding: (1) normative structures based on symmetry, from George Perle; (2) pitch class set theory, from Allen Forte; and (3) transformational networks, from David Lewin. The last two are influenced by the premises of twelve-note theory given by Schoenberg and later expanded on by Babbitt. Each theory, while decidedly non-tonal in approach, defines relationships that have priority over others and govern successions of notes, in ways that are at least remotely analogous to the hierarchies of tonality.
These three theories share some general principles; in particular, two interpretations of melodic and harmonic events in atonal music have proven seminal. The first stems from the recognition that the referential sonorities in atonal music are not triads and that the organization is no longer based on tonal function and the hierarchical organization of key centres. Notes freed from tonal obligations have come to be regarded as enharmonically equivalent and functionally indistinguishable, and generalized into 12 pitch classes. In principle, any group of pitch classes can occur in a chord, melody or combination, and these note-groups may succeed each other without the dependent relationships of tonality. The second interpretation in atonal music is a focus on intervals rather than pitches for relating note-groups. With this change in orientation have come changes in the way intervals are described: they are no longer divided into ‘consonant’ and ‘dissonant’ categories; intervals are named by the number of semitones they contain, rather than by their tonal names; and equivalences of intervals related by octaves (defined as 12 ‘pitch class intervals’), and even by octave complements (those that add up to an octave, defined as six ‘interval classes’), are asserted. Thus, rather than talking about pieces being in keys, writers describe pieces as having intervallic tendencies among non-triad note-groups.
Without the organizing force of a tonic key note and hierarchical grouping and voice-leading between triads, new criteria for classification and relationships among note-groups have also developed: (1) collectional or order equivalence, where a note-group is recognizable as a categorized ‘collection’ when presented in any order, which may include horizontal or vertical; (2) transpositional equivalence, where a note-group is not differentiated functionally from transpositions of itself; (3) inversional equivalence, where a note-group is not differentiated functionally from inversions of itself; and (4) symmetry as a structural property, with mirror symmetry, symmetrical collections (those in which inversions are equivalent to transpositions) and interval cycles acting as alternatives to the chord progressions and voice-leading of tonality. All these criteria relate to ‘invariance’, a central concept in which some aspect of a note-group – either pitch, pitch class, interval or interval class – is retained following some operation.
Many
writers have codified the possible collections available by various intervallic
successions, initially as ‘scales’ for compositional resources and later as
lists of equivalent note-groups. The traditional equivalence operations are
transposition and inversion, where, for instance, the note-groups C–E–G and A–C–E
(transposition) and C–E–G
and C–E–G (inversion) are considered equivalent. A later addition is
equivalence under ‘M’ or multiplicative operations, where ‘M5’- or ‘M7’-related
collections – for example C–C–D and C–F–B at M5, with exchanged interval class 1 and 5 values –
are considered equivalent. Such lists and criteria are often defined using
numbers and mathematical relationships, with C = 0, C/D = 1, … A/B = 10, B = 11 (10 and 11 are also notated variously as
‘t’, ‘e’), with transposition expressed as addition and inversion as
subtraction, and even with geometrical shapes and equations (see O'Connell,
1962, and Roeder, 1987). Some notational conventions are: (1) 〈x, y,
z〉 (〈C, E,
G〉) for unordered collections of pitches or pitch classes, that is, those
in which order is not considered an identifying feature; (2)
〈x–y–z〉 (〈C–E–G〉) for ordered collections of pitches or pitch
classes, that is, those in which order is an identifying feature; and (3) [xyz]
([037]) for a set class, an equivalence class of all unordered pitch class
collections related by transposition or inversion to a representative
note-group, here {C, E,
G}.
A letter from Berg to Schoenberg (27 July 1920), in which Berg outlined his interest in interval cycles and symmetry, is the strongest source evidence for symmetry being an organizing force in atonal music (as asserted by Perle). Perle has described symmetrical procedures in tonal music as ‘windows of disorder’ which become ‘windows of order’ in atonal music.
In
reference to music principally by Berg and Bartók, but also by Schoenberg,
Webern, Stravinsky, Skryabin and others, Perle describes ‘normative’ elements
that underlie the surface in similar ways, stemming from the symmetry of the
12-note equal-tempered collection, which act as priority elements among other
‘reflexive’ or local elements in pieces. This symmetry is manifested as
interval cycles (e.g. ‘3-cycles’ of 〈C–E–F–A〉, 〈C–E–G–B〉 and 〈D–F–A–B〉) and cyclic collections (e.g. {C,
E, F, A} as a collection from the complete
whole-tone collection {C, D, E, F, G, A}), and in inversional complementation (e.g. 〈c'–e'〉
as the complement or mirror pair to 〈d–f〉 around axis note a:
〈d–f–[a]–c'–e'〉).
Symmetry
results not only from the division of musical space into equal-division pitch
space, resulting in ‘mirror symmetry’ and an ‘axis’ of symmetry, but in a more
general sense from relationships among collections of pitch classes (e.g.
〈C–E〉 and 〈D–F〉 expressed numerically as 〈0–4〉
and 〈2–6〉, then related by the sum of complementation 6, from 0+6
[C+F] and 4+2 [E+D]:
Babbitt's term for this sum is ‘index number’). Different symmetrical bases can
combine, with pitches or pitch classes lying both inside and outside the
prevailing symmetrical system(s), or acting as transitions to some new cyclic
aspect of the system, allowing for a hierarchy of symmetrical and
non-symmetrical notes. Where it occurs, symmetry is thus in a constant state of
interruption and regeneration, tension and release, somewhat analogously to
tonal stability and instability by motion away from and back to a tonic key.
The
principal elements of symmetry are: (1) voice-leading and registral motion by
interval cycles, where composition can be motivated to fill gaps within cycles,
span cyclic intervals, transpose or invert cycles, or change to different
cycles; (2) cyclic collections as a harmonic basis, either from pure cycles or
cycles with added ‘dissonant’ notes (e.g. a whole-tone collection plus an added
note C, 〈F–E–D–A–C–B〉, from the
beginning of Berg's String Quartet op.3), with procedures such as transposition
to different cycle forms, changes or reinterpretation in cyclic basis (e.g.
〈C–C–D–E〉
as a 1-cycle 〈C–C–D〉
collection plus E reinterpreted as a 2-cycle 〈C–D–E〉 collection
plus C), and
opposition and reconciliation of cyclic bases; (3) embedded cyclic collections
functioning within larger note-groups, which are influenced by the intervallic
properties of the interval cycle; and (4) a structural role for symmetrical
note-groups, with their transpositional or inversional invariances, and axes of
symmetry or pitch class sums of complementation. Such sums are identified by Perle
as ‘keys’ and used to relate different pieces, such as the sum 9 relationship
pairing E/F, E/F, D/G, D/G, C/A and B/B (in numbers, 4/5, 3/6, 2/7, 1/8, 0/9, 11/10 (mod 12))
between the first movements of Berg's Lyric Suite and Bartók's Fourth String
Quartet.
Pitch
class set theory, as set out principally by Forte, establishes a theoretical
context in which pitches are grouped into pitch class sets, which are then
further categorized into set classes equivalent under transposition and
inversion. Set classes are labelled by cardinality, placement within a list
ordered by interval class content and prime form (e.g. set class 4–1 [0123]
indicates four notes, e.g. {C, C, D, D}, with its interval class ‘vector’ of
〈321000〉 identifying three interval class 1s, two interval class 2s
etc., placed first in the list of four-note set classes, and with a prime or
most compact form [0123]). Set classes grouped or ‘segmented’ in analyses of
pieces are related to each other in several ways: in ‘literal’ relationships
two sets share pitch classes; in ‘abstract’ relationships two sets share
interval classes. Two other relationships are the ‘complement’ of a set, which
may be a literal complement consisting of the remaining pitch classes or the
abstract complement consisting of the set class of the remaining pitch classes,
and a ‘Z-relation’, in which two set classes of the same cardinality have the
same interval class vector but not the same prime form (e.g. [0137] and [0146],
both with vector 〈111111〉).
The organization of atonal pieces is interpreted by a hierarchical network relating as many set classes as possible to a central ‘nexus’ set – a set, usually a hexachord, that shares the greatest number of interval class relationships with surrounding sets and their complement sets. Two types of network exist: (1) a ‘K’ network, which results when, among two set classes of different cardinalities, S and T, and their complements S' and T', S is a subset or superset of either T or T'; and (2) a more exclusive ‘Kh’ network, yielding a smaller number of related sets, which results when set class S is a subset or superset of both set classes T and T'.
Many
writers have expanded on pitch class set theory to show the ‘normative’
elements that result from the 12-note equal-tempered system: (1) the equivalent
invariance properties and intervallic structures of complementary sets, where
interval class vector entries differ by the difference in cardinalities (e.g.
given set class 3–1 {C, C, D} vector 〈210000〉 and complement 9–1
{D, E, F, F, G, G, A, A, B} vector 〈876663〉, 876663
− 210000 = 666663, with the interval class 6 entry halved due to its
invariance); (2) the tendency of hexachords to be nexus sets; (3) the presence
of Z-related pairs of sets; and (4) the similarity of relationships, sharing
pitch class and interval class content, between pitch class sets, usually
expressed as percentages in a scale of 0 to 1. These ‘normative’ structures
provide a context for the ‘reflexive’ elements of individual pieces. See
also Set.
Lewin's focus has been on the spans between musical events rather than on the events themselves – durations rather than attacks, intervals rather than pitches. These spans, called ‘intervals’ in a more generalized sense, are regarded as active rather than passive, transformational rather than simply measurable or classifiable, ordered in time and space, and interpretable according to relative, rather than absolute, criteria. By combining defined musical spaces (‘S’, e.g. pitch), a group of mathematical operations (IVLS, e.g. the addition of semitones), and defined mappings of objects on to one another by specific intervals (a function ‘int’ mapping s on to t, e.g. transposition), Lewin's analytical apparatus, the Generalized Interval System (GIS), can encompass aspects of many existing theories of atonal and tonal music. The successive intervals transforming one object through a succession of other objects are displayed in transformational networks, which are internally ordered and logical, and to varying extents independent of the objects being transformed.
In
practice, Lewin's analyses are governed by several premises. Like Perle, Lewin
defines intervals both as differences (transpositions) and sums (inversions).
Inversion is described in terms of inversional ‘balance’, manifested as either
pitch axes or pitch class sums that group surrounding notes (e.g. the axis A/B groups note pairs A/B, G/B, G/C, F/C, F/D and E/E. The completion of either a pitch-inversional dyad in
register or of a pitch class-inversional pair is often a compositional premise.
Intervals are regarded as having tendencies to propagate themselves as
transpositional or inversional levels. Lewin allows for the equivalences of
pitch class set theory, and combines transposition and inversion within the
same set as ‘Klumpenhouwer networks’ (e.g. 〈A–F–B〉 with interval 2 〈A–B〉
transposed to 〈A–B〉, and interval
〈A–F〉
symmetrically expanded at sum 3 to 〈A–G〉 to yield 〈A–G–B〉), analogous to Perle's combinations of sum and
difference relationships in the ‘cyclic sets’ that are the basis of his 12-note
tonality. Analytically, Lewin stresses pitch relationships with registral
extremes or boundary notes as significant elements.
Noteworthy in analytical commentary from Lewin's approach are the following: aggregates and aggregate completion; instances of symmetrical pitch inversion as more ‘audible’ realizations of pitch class inversional complementation; axis notes of inversion occurring as adjacent notes in a series; and ordered relations among symmetrically related notes. The point of the analysis is often to relate as many collections as possible by a similar set of transformations – particularly to show that different collections, whether symmetrical or asymmetrical, adjacent or divided on the surface by register, have similar transformational relationships – and in this way to demonstrate the underlying unifying principles that connect the first note to the last in a passage. A transformational scheme is valued for including virtually every note, and is validated by recurring ‘motivic’ pitch registral connections on the surface and in relation to other movements.
Atonality thus roughly delimits a wide range of compositional practices whose only features are the absence of the normative and interrelated procedures of tonality and of the basic concept of serialism. It remains to be seen to what extent atonality is a useful or relevant musical category. The tendency of historical criticism to construct systems of classification which attempt to index individual entries as neatly and unambiguously as possible has certainly been frustrated so far. The individuality of the contributions of Schoenberg, Stravinsky, Bartók, Webern, Berg and others ultimately transcends and trivializes such attempts, if it does not contradict them.
B. Ziehn: Harmonie- und Modulationslehre (Berlin, 1887–8; Eng. trans., 1907)
A. Schoenberg: Harmonielehre (1911, 3/1922; Eng. trans., 1978)
B. Ziehn: Five- and Six-Part Harmonies and How to Use Them (Milwaukee, 1911)
E. Bacon: ‘Our Musical Idiom’, The Monist, xxvii (1917), 560–607
H. Eimert: Atonale Musiklehre (Leipzig, 1924)
F.H. Klein: ‘Die Grenze der Halbtonwelt’, Die Musik, xvii/4 (1925), 281–6
A. Hába: Neue Harmonielehre des diatonischen, chromatischen, Viertel-, Drittel-, Sechstel-, und Zwölftel-Tonsystems (Leipzig, 1927)
H. Cowell: New Musical Resources (1930/R)
A. Schoenberg: ‘Analysis of the Four Orchestral Songs Opus 22’ [1932], PNM, iii/2 (1964–5), 1–21; repr. in B. Boretz and E.T. Cone, eds.: Perspectives on Schoenberg and Stravinsky (Princeton, NJ, 1968, 2/1972), 25–45
A. Schoenberg: ‘Problems of Harmony’, MM, xxi (1934), 167; repr. in Style and Idea (New York, 1950, 3/1984), 268–87
A. Berg: ‘Was Ist atonal?’, 23: eine wiener Musikzeitschrift, vi–vii (1936), 1–11; Eng. trans. in N. Slonimsky: Music since 1900 (New York, 1938, 5/1994), 1027–9
P. Hindemith: Unterweisung im Tonsatz (Mainz, 1937–9, 2/1940; Eng trans., 1941–2, 2/1948)
J. Schillinger: Kaleidophone: New Resources of Melody and Harmony (New York, 1940)
O. Messiaen: Technique de mon langage musical (Paris, 1944; Eng. trans., 1956)
F. Salzer: Structural Hearing: Tonal Coherence in Music (New York, 1952)
D. Lewin: ‘Intervallic Relations between Two Collections of Notes’, JMT, iii (1959), 298–301
R. Travis: ‘Toward a New Concept of Tonality?’, JMT, iii (1959), 257–84
H. Hanson: Harmonic Materials of Twentieth-Century Music (New York, 1960)
W. O'Connell: ‘Der Ton-Raum’, Die Reihe, viii (1962), 35–61; Eng. trans. in Die Reihe, vii (1968), 34–67
G. Perle: Serial Composition and Atonality (Berkeley, 1962, 6/1991)
A. Berger: ‘Problems of Pitch Organization in Stravinsky’, PNM, ii/1 (1963–4), 11–42
A. Forte: ‘A Theory of Set-Complexes for Music’, JMT, viii (1964), 136–83
J. Tenney: Meta/Hodos and META Meta/Hodos (New Orleans, 1964)
J. Clough: ‘Pitch-Set Equivalence and Inclusion (A Comment on Forte's Theory of Set-Complexes)’, JMT, ix (1965), 163–71
R. Teitelbaum: ‘Intervallic Relations in Atonal Music’, JMT, ix (1965), 72–127
E. Carter: ‘Expressionism and American Music’, PNM, iv/1 (1965–6), 1–13
R. Travis: ‘Directed Motion in Schoenberg and Webern’, PNM, iv/2 (1965–6), 85–9
G. Perle: ‘The Musical Language of Wozzeck’, Music Forum, i (1967), 204–59
D. Lewin: ‘Inversional Balance as an Organizing Force in Schoenberg's Music and Thought’, PNM, vi/2 (1967–8), 1–21
R. Craft: ‘Schoenberg's Five Pieces for Orchestra’, Perspectives on Schoenberg and Stravinsky, ed. B. Boretz and E.T. Cone (Princeton, NJ, 1968, 2/1972), 3–24
B. Boretz: ‘Meta-Variations: Studies in the Foundation of Musical Thought’, PNM, viii/1 (1969–70), 1–74; viii/2 (1969–70), 49–111; xi/1 (1972–3), 146–233; xi/2 (1972–3), 156–203
B. Boretz: ‘The Construction of Musical Syntax (I)’, PNM, ix/1 (1970–71), 23–42
J. Maegaard: Studien zur Entwicklung des Dodekaphonene Satzes bei Arnold Schönberg (Copenhagen, 1972) [review in MQ, lxiii (1977), 273]
A. Forte: ‘Sets and Nonsets in Schoenberg's Atonal Music’, PNM, xi/1 (1972–3), 43–64
A. Forte: The Structure of Atonal Music (New Haven, CT, 1973)
B. Alphonse: The Invariance Matrix (diss., Yale U., 1974)
E. Cone: ‘Sound and Syntax: an Introduction to Schoenberg's Harmony’, PNM, xiii/1 (1974–5), 21–40
E. Regener: ‘On Allen Forte's Theory of Chords’, PNM, xiii/1 (1974–5), 191–212
P. Lansky: ‘Pitch-Class Consciousness’, PNM, xiii/2 (1974–5), 30–56
C. Gamer and P. Lansky: ‘Fanfare for the Common Tone’, PNM, xiv/2–xv/1 (1976), 229–35
R. Chrisman: ‘Describing Structural Aspects of Pitch-Sets using Successive-Interval Arrays’, JMT, xxi (1977), 1–28
D. Lewin: ‘Forte's Interval Vector, My Interval Function, and Regener's Common-Note Function’, JMT, xxi (1977), 194–237
G. Perle: ‘Berg's Master Array of the Interval Cycles’, MQ, lxiii (1977), 1–30
A. Chapman: A Theory of Harmonic Structure for Nontonal Music (diss., Yale U., 1978)
D. Starr: ‘Sets, Invariance, and Partitions’, JMT, xxii (1978), 1–42
D. Beach: ‘Pitch Structure and the Analytic Process in Atonal Music: an Interpretation of the Theory of Sets’, Music Theory Spectrum, i (1979), 7–22
D. Lewin: ‘A Response to a Response: on Pcset Relatedness’, PNM, xviii (1979–80), 498–502
R. Morris: ‘A Similarity Index for Pitch-Class Sets’, PNM, xviii (1979–80), 445–60
J. Rahn: ‘Relating Sets’, PNM, xviii (1979–80), 483–98
G. Perle: The Operas of Alban Berg, i: Wozzeck (Berkeley, 1980)
J. Rahn: Basic Atonal Theory (New York, 1980)
J. Tenney and L. Polansky: ‘Temporal Gestalt Perception in Music’, JMT, xxiv (1980), 205–41
A. Forte: ‘The Magical Kaleidoscope: Schoenberg's First Atonal Masterwork, opus 11, no.1’, Journal of the Arnold Schoenberg Institute, v (1981), 127–68
C. Hasty: ‘Segmentation and Process in Post-Tonal Music’, Music Theory Spectrum, iii (1981), 54–73
C. Lord: ‘Intervallic Similarity Relations in Atonal Set Analysis’, JMT, xxv (1981), 91–111
R. Morris: ‘Review of John Rahn's Basic Atonal Theory’, Music Theory Spectrum, iv (1982), 138–54
R. Morris: ‘Set Groups, Complementation, and Mappings among Pitch-Class Sets’, JMT, xxvi/1 (1982), 101–44
M. Kielian-Gilbert: ‘Relationships of Symmetrical Pitch-Class Sets and Stravinsky's Metaphor of Polarity’, PNM, xxi (1982–3), 209–40
D. Lewin: ‘Transformational Techniques in Atonal and Other Music Theories’, PNM, xxi (1982–3), 312–71
R. Morris: ‘Combinatoriality without the Aggregate’, PNM, xxi (1982–3), 432–86
J. Baker: ‘Schenkerian Analysis and Post-Tonal Music’, Aspects of Schenkerian Theory, ed. D. Beach (New Haven, CT, 1983)
J. Clough: ‘Use of the Exclusion Relation to Profile Pitch-Class Sets’, JMT, xxvii (1983), 181–201
J. Schmalfeldt: Berg's ‘Wozzeck’: Harmonic Language and Dramatic Design (New Haven, CT, 1983)
E. Antokoletz: The Music of Béla Bartók (Berkeley, 1984)
C. Hasty: ‘Phrase Formation in Post-Tonal Music’, JMT, xxviii (1984), 167–90
G. Perle: ‘Scriabin’s Self-Analyses’, MAn, iii (1984), 101–22
A. Forte: ‘Pitch-Class Set Analysis Today’, MAn, iv (1985), 29–58
J. Bernard: The Music of Edgard Varèse (New Haven, CT, 1987)
D. Lewin: Generalized Musical Intervals and Transformations (New Haven, CT, 1987)
R.D. Morris: Composition with Pitch-Classes: a Theory of Compositional Design (New Haven, CT, 1987)
J. Roeder: ‘A Geometric Representation of Pitch-Class Series’, PNM, xxv (1987), 362–409
J. Straus: ‘The Problem of Prolongation in Post-Tonal Music’, JMT, xxxi (1987), 1–21
A. Forte: ‘New Approaches to the Linear Analysis of Music’, JAMS, xli (1988), 315–48
A. Forte: ‘Pitch-Class Set Genera and the Origin of Modern Harmonic Species’, JMT, xxxii (1988), 187–270
R. Wason: ‘Tonality and Atonality in Frederick Rzewski's Variations on “The People United Will Never Be Defeated”’, PNM, xxvi/1 (1988), 108–43
A. Mead: ‘The State of Research in Twelve-Tone and Atonal Theory’, Music Theory Spectrum, xi (1989), 40–48
J. Roeder: ‘Harmonic Implications of Schoenberg's Observations of Atonal Voice Leading’, JMT, xxxiii (1989), 27–62
J. Baker: ‘Voice Leading in Post-Tonal Music: Suggestions for Extending Schenker's Theory’, MAn, ix (1990), 177–200
D. Lewin: ‘Klumpenhouwer Networks and Some Isographies that Involve Them’, Music Theory Spectrum, xii (1990), 83–120
G. Perle: The Listening Composer (Berkeley, 1990)
G. Perle: ‘Pitch-Class Set Analysis: an Evaluation’, JM, viii (1990), 151–72
J. Straus: Introduction to Post-Tonal Theory (Englewood Cliffs, NJ, 1990)
J. Straus: Remaking the Past: Musical Modernism and the Influence of the Tonal Tradition (Cambridge, MA, 1990)
E.W. Marvin: ‘The Perception of Rhythm in Non-Tonal Music: Rhythmic Contours in the Music of Edgard Varèse’, Music Theory Spectrum, xiii (1991), 61–78
S. Neff: ‘An American Precursor of Non-Tonal Theory: Ernst Bacon (1898–1990)’, CMc, no.48 (1991), 5–26
D. Headlam: ‘Fritz Heinrich Klein's “Die Grenze der Halbtonwelt” and Die Maschine’, Theoria, vi (1992), 54–96
D.W. Bernstein: ‘Symmetry and Symmetrical Inversion in Turn-of-the-Century Theory and Practice’, Music Theory and the Exploration of the Past, ed. C. Hatch and D.W. Bernstein (Chicago, 1993), 377–407
R. Morris: ‘New Directions in the Theory and Analysis of Musical Contour’, Music Theory Spectrum, xv (1993), 205–28
G. Perle: ‘Communication (Re: Lewin, “Klumpenhouwer Networks”)’, Music Theory Spectrum, xv (1993), 300–03
R. Morris: ‘Recommendations for Atonal Music Pedagogy in General; Recognizing and Hearing Set-Classes in Particular’, Journal of Music Theory Pedagogy, viii (1994), 75–134
G. Perle: The Right Notes (Stuyvesant, NY, 1995)
E. Haimo: ‘Atonality, Analysis, and the Intentional Fallacy’, Music Theory Spectrum, xviii (1996), 167–99
J.W. Bernard: ‘Chord, Collection, and Set in Twentieth-Century Theory’, Music Theory in Concept and Practice, ed. J.W. Baker, D.W. Beach and J.W. Bernard (Rochester, NY, 1997), 11–51
G. Perle: ‘Berg’s Style of Freedom’, MT, cxxxix (1998), 12–31