); and ‘R’ indicates the retrograde of the
cited series.A method of composition in which a fixed permutation, or series, of elements is referential (i.e. the handling of those elements in the composition is governed, to some extent and in some manner, by the series). Most commonly the elements arranged in the series are the 12 notes of the equal-tempered scale. This was so in the technique introduced by Schoenberg in the early 1920s and employed by him in most of his subsequent compositions. Serialism was quickly taken up by his pupils, including Berg and Webern, and then by their pupils, but not at first by many outside this circle, the most important exceptions being Dallapiccola and Krenek. The method spread more widely and rapidly in the decade after World War II, when Babbitt, Boulez, Nono and Stockhausen produced their first acknowledged works. These composers and their colleagues sometimes extended serialism to elements other than pitch, notably duration, dynamics and timbre. At the same time serial techniques began to be used by already established composers; here the outstanding example was Stravinsky. The diverse range of composers so far mentioned should indicate that serialism cannot be described as constituting by itself a system of composition, still less a style. Nor is serialism of some sort incompatible with tonality, as is demonstrated in works by Berg and Stravinsky, for example, though it has most usually been employed as a means of erecting pitch structures in atonal music.
3. Serialism with other pitch-class collections.
PAUL GRIFFITHS
In 12-note serialism (sometimes referred to as ‘dodecaphony’, a term which is ambiguous in that it can refer to non-serial atonal music) the series is an ordering of the 12 notes of the equal-tempered chromatic scale (i.e. the 12 pitch classes) so that each appears once. Such a series can exist at 12 transpositional levels, all of which Schoenberg considered to be forms of the same series, and he also included the inversion, the retrograde and the retrograde inversion at each transpositional level in the complex, so that the series may be used in any of 48 forms. Thus the constant reference is a series of 11 interval classes in any of four shapes – prime, retrograde, inversion and retrograde inversion – at any of 12 transpositional levels. This is the understanding of the series that most later composers have accepted.
There
is no standard convention for naming serial forms. That used here is as
follows: ‘P’ indicates prime and ‘I’ inversion; the subscript numeral is the
pitch-class number of the initial pitch class, i.e. the number of interval
classes of a semitone by which the initial pitch class is raised above C (e.g.
‘10’ indicates a series beginning with B); and ‘R’ indicates the retrograde of the
cited series.
The basic convention in serial composition is that the pitch successions in any portion of the music should be the whole or part of one or more statements of a series. This leaves undefined the registers at which the pitch classes are presented (and questions of change in register from one serial statement to another), what part of the series is projected linearly and what part vertically, how many statements of the series are made concurrently, to what extent each polyphonic voice presents its own sequence of serial statements, how many different series are used (and, if more than one, how they are related, if at all), and how, if at all, concurrent or consecutive serial statements are linked, in nature (e.g. by having I6 follow P0) and/or compositional usage (e.g. by shared notes). The examples that follow suggest some of the practices in these areas established by different composers. It is important to note that these practices are not restricted to the composers in whose work they are demonstrated, and that the composers concerned are/were not restricted to the particular practices described. Further observations will be found under Twelve-note composition.
Serialism, §2: 12-note serialism
The Variations for Orchestra op.31 (1928) afford a compendium of Schoenberg's early serial technique. The Hauptstimme of the theme (bars 34–57) presents four linear statements of the series in the forms P10–I7R–P10R–I7; such a use of one or more serial statements as a melodic theme is found in many others of Schoenberg’s serial works. Ex.1 shows the first two forms in this instance. Note that the two are identical in hexachordal content. It is clear, therefore, that the first hexachord of I7 has no pitch class in common with the first hexachord of P10; or, to put it another way, these two hexachords together form a 12-note aggregate (or the ‘chromatic total’), that is, they are complementary. Where this situation obtains, the series is said to exhibit the property of combinatoriality, specifically of inversional hexachordal combinatoriality (see Set). Many of Schoenberg's series are of this (specific) type, and he exploited the property when associating serial forms. Thus the four forms of the theme’s Hauptstimme are chosen and arranged so that, with one exception, complementary hexachords are adjacent. If x and y, in that order, represent the hexachordal contents of P10, then this line presents x–y–x–y–y–x–y–x.
The property of combinatoriality also conditions the association of simultaneous serial forms in the theme of op.31. Thus P10 is accompanied by I7, I7R by P10R, P10R by I7R and I7 by P10: each form is accompanied by its inversional hexachordal combinatorial partner. As often in Schoenberg, these relationships are to some extent hidden. Only at the statement of P10R accompanied by I7R is hexachordal partitioning made explicit: the hexachords of P10R are presented as separate phrases and those of I7R as three-note chords – successive in the case of the first hexachord, overlapping in the case of the second – so that y (line) is accompanied by x (chords) and then x (line) by y (chords), that is, complementary hexachords are aligned. In the remaining three serial statements of the Hauptstimme, the phrases are other than hexachordal and so are the accompanying chords (there is almost, but not quite, an identity between the numbers of pitches in the phrases and the numbers of pitches in the chords).
One
final point before leaving these 24 bars. In the last six of them there is a Nebenstimme
stating P1. Reference to ex.1 will show that the series
contains two intervals of the tritone class (in the case of P10
these are B–E and C
–G) and that the four
pitch classes involved in these intervals together form a diminished 7th chord.
Since this chord divides the octave into equal parts of a minor 3rd, any two
serial forms (of which either or both may be P or I) separated from each other
by one or more interval classes of a minor 3rd will contain the same four pitch
classes at the tritone intervals (i.e. at positions 1, 2, 8 and 9; or, in
retrograde forms, 4, 5, 11 and 12), though, of course, the pitch classes will
be reordered; in other words, the unordered set of pitch classes in these
positions is invariant under the conditions stated. Thus, to return to the
particular case at the close of the theme, P1 is related to the four
forms announced in the Hauptstimme by this invariant relation.
Furthermore, a special association links P1 with the Hauptstimme
form with which it is concurrent, namely I7: this pair is one of
those that holds the ordering at two (the maximum) of the positions under
discussion (here 8 and 9) invariant.
Association through an invariant unordered set at the tritone intervals occurs elsewhere in the composition – for example at the beginning (bars 58–62) of the first variation, where a statement of P10 is accompanied by P1, P10, I1 and I10. Moreover, these four forms in the accompaniment are presented in homophonic pairs, P1/P10 and I1/I10, so that they produce a preponderance of vertical intervals of the minor-3rd class (minor 3rds and minor 10ths) or of a major 6th (which is related to the minor-3rd class by octave displacement), so drawing attention to the interval class that governs not only the invariant relation described here but also the combinatorial relation (combinatorially related forms, such as P10 and I7, are separated by the interval class of a minor 3rd).
In the examples given so far, each ‘voice’ (which may be linear or chordal) is assigned one or more complete serial forms. This is by no means always the case in Schoenberg. At the opening of the third variation of op.31, for instance, the Hauptstimme is an ostinato of six-note tritone figures derived from the series as shown in ex.2; the other pitch classes of the series are filled in severally by other instruments. In addition, the forms used to generate these tritone figures are in tritone relations with each other: I7–P1–I1–P7 (bars 106–9) and P10R–I10R–P4R–I4R (bars 111–14). During the bars in question two horns are presenting the melody or theme (with rhythmic modification) so that P10 is associated with the first group and I7R with the second. The relationships of symmetry, invariance and combinatoriality that exist within and between these groups, each of five forms, can readily be discerned.
It is impossible to illustrate here all the means used by Schoenberg in associating serial forms in op.31, still less in his work as a whole; but the principles of combinatoriality and invariance are almost always of fundamental importance. In some later compositions, notably the Violin Concerto op.36, the Fourth String Quartet op.37 and the Piano Concerto op.42, he elaborated relations between serial statements and associations among them, on the analogy of the long-term techniques of tonal composition, to assure the coherence of extended forms. His handling of serialism was almost always based on tonal models in matters of form (sonata and variations in particular) and texture (theme and accompaniment), even if it would be difficult to find a precedent – outside his own tonal works – for the richly polyphonic character of his writing. The String Trio op.45 and the Phantasy op.47, however, exhibit forms that are not so readily referable to conventional patterns.
Schoenberg’s
later works also show a relaxation of serial convention. Not only did he return
to tonal methods for whole compositions, but within non-tonal pieces he
admitted tonal features that he had previously avoided, such as vertical
octaves and even diatonic triads: the Ode to Napoleon op.41 ends in E. This work is a somewhat
extreme example, in that it cannot be considered strictly serial at all, since
reorderings of pitch classes within hexachords are permitted; in other words,
its basic set is not a series but a hexachordal trope. Such reorderings also
occur in, for example, the String Trio, but to a lesser extent.
Serialism, §2: 12-note serialism
If Schoenberg’s serial practice became, in some respects, increasingly liberal, Berg’s was never anything but free. In no work – indeed, in no movement – did he keep to a single series. The first movement of the Lyric Suite for string quartet (1926), for instance, is based not on a series but on the succession of 5ths beginning on F (ex.3). This is first presented (bar 1) as three four-note chords but, as in Schoenberg, partitioning into hexachords is more important. Reordering within the hexachords produces the series shown in ex.4, which is presented in the Hauptstimme of bars 2–4. It is an ‘all-interval series’, that is, a series which, in any one form, contains an interval of each class except the unison. Examination of the series will show that it also has the property of inversional hexachordal combinatoriality, though this is not exploited in the composition, nor in Berg’s music generally. Cyclic permutation of ex.4 produces another series (ex.5: the last four pitch classes of ex.4 here become the first four), which is heard in the Hauptstimme of bars 7–9. A third series, first presented in bar 33, is generated by reordering the hexachords of ex.3 so that interval-class size is minimal (ex.6).
It is clear that Berg’s licences with Schoenbergian convention produce series of quite diverse types within one movement, and in larger works, notably the opera Lulu, reordering is more extensively applied. In addition, Berg often used pitch material unrelated to the set, frequently resorting to tonal practice (most notably in the Violin Concerto), and he made independent use of fragments of serial statements. However, if he employed more freely than did Schoenberg non-standard serial transformations (cyclic permutation etc.), he limited his choice from the conventional 48 forms. In particular, retrograde forms are rare in his music outside sections that are retrograded as a whole (as, for example, in Der Wein). Furthermore, the thematic character of the series is emphasized by a limitation of octave displacement from one serial statement to another (the series shown in ex.6, for example, is always stated with its intervals conjunct), and series of different type are projected in a manner that keeps other aspects constant (for instance, the first appearances of exx.4 and 5 are both in the first violin and in very similar rhythms).
Serialism, §2: 12-note serialism
By contrast with Schoenberg and Berg, Webern always used a single series for each composition (counting the numbers of opp.17 and 18 as separate compositions), he drew only on the standard 48 forms, he rarely repeated notes or groups of notes within serial statements after opp.17–20, and he almost never presented the series as a melodic theme in a constant timbre. Another distinctive feature of Webern’s serialism is the use of highly symmetrical series. That of the String Quartet op.28 (1938), shown in ex.7, is typical. The second hexachord is the retrograde inversion of the first transposed by an interval class of a major 6th, so that Pn = In+9R; thus there are only 24 different forms of the series. Moreover, the three tetrachords of the series are in the relation p0–p4r–p8 (i.e. the second tetrachord is the retrograde of the first transposed by an interval class of a major 3rd, and the third is the first transposed by an interval class of a minor 6th); thus transposition of a serial form by one or more interval classes of a major 3rd will generate a serial form containing the same tetrachords in different positions and with two of the three retrograded.
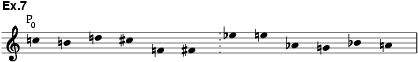
This property of different serial forms having the same content of tetrachords is used at the opening of the first movement, the first three serial statements being of P7, P3 and P11 (obviously, any or all of these names might be replaced by IR ones, given the symmetrical property described). Each adjacent pair is linked by terminal tetrachords held in common, as shown in ex.8. Linking serial forms through common terminals is a frequent practice in Webern from op.21 onwards, but the shared notes are most usually one or two in number; this technique may limit, of course, the range of serial statements that can be chosen to follow a given form. Before leaving ex.8 it should be noted that the three serial forms there shown are in the relation of prime tetrachordal combinatoriality; that is, a 12-note aggregate is formed by all of the first or second or third tetrachords. However, Webern did not normally make explicit use of the combinatorial relations in which his symmetrical series are rich. The vertical association of serial forms in the first movement of op.28 (which is, from bar 16 on, composed in two-part canon) is rather of the type Pn with Pn+3, which can, given the symmetrical relation, be written InR with Pn; and consecutive association in this movement is governed, as hinted above, by the property of terminal invariance, Pn having four notes in common with Pn+8 following or two notes in common with Pn+10R following.
The opening quadruple canon of the second movement (bars 1–18) shows tetrachordal invariance at its most pervasive – the passage makes use of only six serial forms, P0, P4, P8 and their retrogrades, and therefore of only three tetrachords of different content – and suggests how much Webern’s serialism was conditioned by symmetry and coincidence.
Serialism, §2: 12-note serialism
The composer who has been most consistent in theoretically codifying and compositionally proceeding from the work of the first-generation serial composers is Babbitt. Two notions central to his serialism – the secondary set and the derived set – were developed from the practices, respectively, of Schoenberg and Webern; and he made considerable and extended use of combinatoriality. Something of these features can be illustrated in a short passage (bars 266–75) of the Second String Quartet (1954). This passage opens with a statement of the principal series in the form P8 (ex.9) by all four instruments, after which the first violin and the viola present I5 (ex.10). These two forms are in the relation of inversional hexachordal combinatoriality. The presence of that property makes it possible for a new 12-note series to be formed of complementary hexachords from different serial forms; such a series is termed by Babbitt a ‘secondary set’. (In ex.1, from Schoenberg, a secondary set is formed by the second hexachord of P10 followed by the first hexachord of I7R.) While the statement of I5 is in progress, a secondary set (ex.11) is presented by the second violin and the cello. Examination will show that ex.11 is constituted from the second hexachord of I11R and then the first of P2.
It is evident that these two forms, I11R and P2, are identical with each other in hexachordal content and that both are hexachordally combinatorial with P8. Where, as here, a P form has I, IR and P combinatorial partners (any serial form will, of course, be hexachordally combinatorial with its own retrograde), the series is said to be ‘all-combinatorial’. The use of hexachordal combinatoriality to govern the succession and superposition of serial forms at the beginning of the passage under discussion is shown by ex.12, where (a) indicates a hexachord of content identical with that of the first hexachord of P8 and (b) one of complementary content. The presence of secondary sets is obvious from the example.
One item has been left out of account in ex.12: in bars 271–2 the cello presents a 12-note series (ex.13) which is neither a form of the principal series nor a secondary set. Note that its constituent trichords are in the relation p10–i9r–i3–p4r (these names are analogous to those used in considering the symmetrical structure of the series of Webern’s op.28). The first trichord is found in one form of the principal series, P3R, where it occurs in positions 2–4 (ex.14). A series formed by taking an element (of two, three, four or six pitch classes) from a serial form and building from it, by serial transformations, a new 12-note succession is termed a ‘derived set’, and so ex.13 is a derived set in relation to the principal series. Note, too, that it has the hexachordal contents (a)(b).
Derived sets and combinatoriality can be further exemplified in the portion that immediately follows that shown in ex.12 (see ex.15). The series presented by the first violin is a derived set based on the trichord at positions 10–12 of I3 of the principal series, that presented by the second violin is a derived set based on the trichord at positions 4–6 of P11 of the principal series, and that presented by the cello is a derived set based on the trichord at positions 1–3 of I10 of the principal series. The viola presents a principal-serial form, I11R. Solid boxes indicate some of the combinatorial relations, both trichordal and hexachordal, operating here; the dotted box indicates the central tetrachord held invariant between the two violins. Note that the middle interval class in these four series is in each case the tritone.
The ways in which Babbitt has used properties of the series to project large forms can only be suggested here, taking again as example the Second String Quartet. The principal series, of which forms are shown in exx.9, 10 and 14, is an all-interval one, the intervals being, in semitone classes, 3–8–5–9–1–6–2–7–4–10–11. At the opening a derived set based on the first interval class, that of the minor 3rd, is presented (ex.16), followed by a derived set based on the second interval class, that of the minor 6th. This is succeeded by a derived set based on the trichord formed by these two interval classes (ex.17), a set which is used to build bars 7–18. Then the third interval class is introduced, again in a derived set, and then a derived set based on the trichord formed by the second and third interval classes. The composition proceeds in this manner until the first six interval classes have been introduced, when the first hexachord of the principal series is presented by the second violin solo ff (bar 114). In the second half of the quartet the second hexachord of the principal series is established in like manner, the whole principal series appearing for the first time in bars 266–8 (i.e. at the beginning of the passage considered above). This is, of course, no more than a simplified outline of the pitch connections that exist in the work.
Serialism, §2: 12-note serialism
In few of Boulez’s compositions is it an easy matter to demonstrate throughout how the series is referential, and he has developed procedures, such as ‘chord multiplication’, which increase the hazardousness of such demonstration. However, the section ‘Texte’ from the ‘formant’ Trope of the Third Piano Sonata (1957) is of relatively straightforward serial facture, while at the same time it suggests the freedom of his practice. ‘Texte’ is based on a ‘cantus firmus’ formed by four overlapping statements of the series (ex.18); the similarity with Webern’s method of linking statements in op.28 is obvious. This chain of statements returns to the opening tetrachord: the idea of cyclic structure is essential to Trope (whose sections may be cyclically permuted) and to each part of it. The dotted lines in ex.18 divide each serial statement into sets of four types, of which three are related in that a is equivalent in content to b + d transposed by an interval class of a minor 3rd for any given serial statement. Thus the ‘cantus firmus' contains 13 of these sub-serial sets, each of which forms the basis for a defined section of ‘Texte’.
In decorating the ‘cantus firmus’ set in each section, choice is made from other statements of the series, so that each section is built up of the pitch classes of one serial statement, often with note repetitions. Ex.19, from the opening of ‘Texte’, shows the appearances of the first two sets of the ‘cantus firmus’ (circled notes), and the serial forms with which they are associated. Note that these forms are defined not by order but by the compositional projection of their constituent sets (of the types a, b, c and d). The combination of freedom of choice and order in these ‘superstructure’ serial forms with strict order in the ‘cantus firmus' is typically Boulezian.
Composition with series containing a number of pitch classes greater or lesser than 12 was practised by Schoenberg in some movements of the Five Piano Pieces op.23 and the Serenade op.24 (both 1920–23), works which also contain some of the earliest examples of 12-note serial composition. Op.23 no.2, for example, uses a series of nine different pitch classes, though pitch material unrelated to this also occurs; and op.24 no.3 is based on a 14-note series in which three pitch classes are each duplicated. In the former example transpositions of the series are present, but I and IR forms appear only in the last six bars and R forms not at all; on the other hand, op.24 no.3 makes use of P, R, I and IR forms, but at only one transpositional level.
Stravinsky employed series of fewer than 12 pitch classes in several works after and including the Cantata (1951–2) before fully adopting 12-note serialism in Threni (1957–8). The strictest of these in serial usage is In memoriam Dylan Thomas (1954), whose series consists of five different pitch classes. Post-Schoenberg examples of composition with series of more than 12 pitch classes include Berio’s Nones for orchestra (1954). This is based on a 13-note series (ex.20) consisting of two overlapping heptachords, of which the second is the retrograde inversion of the first.
Few composers have attempted to extend serialism to pitch systems other than the equal-tempered semitonal, but Boulez has described a method for deriving quarter-tone series from semitone series, and his cantata Le visage nuptial (1946, revised 1950–51) makes use of quarter-tone serialism in parts and to some extent.
The use of ordered patterns of durations appears in Berg (Lyric Suite, third movement) and Webern (notably in the Variations op.30 for orchestra, 1940). Berg’s rhythmic series is made up of 12 durations, each of one, two or three units; Webern employed two four-item series (ex.21). Both used the series in exact retrogrades, varied them by filling in parts of durations with rests, and ‘transposed’ them by multiplying all values by the same integer. There are, of course, precedents for these procedures, and only the Berg example – by reason of its length and its use of rhythmic order independent of pitch succession – seems to represent an attempt to find an analogue for pitch-class serialism in the rhythmic domain.
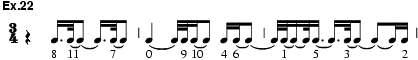
Boulez, who had been working towards the serialism of durations in several works of the late 1940s, employed a systematic method in Structures Ia for two pianos (1952). His notion of a ‘chromatic’ duration series – one consisting of 12 values, each a different whole number of demisemiquavers from one to 12 – came from Messiaen’s Mode de valeurs et d’intensités for piano (1949), where the use of the duration set (and sets governing other aspects) is not serial. In the Boulez example, however, the set is employed as a series. The order numbers of the pitch classes in the serial form P3 (i.e. the numbers from 0 to 11 assigned to them in the order in which they appear in that serial form) are retained by those pitch classes in the 47 other serial forms. This produces 48 orderings of the numbers 0–11 which can be used to generate 48 orderings of the integral durations from one to 12 demisemiquavers by adding one to each order number and expressing the result in demisemiquavers. The duration-serial forms are used independently of the corresponding pitch-class-serial forms (otherwise the same pitch class would always be associated with the same duration).
Such interpretations of rhythmic serialism are problematic. There is no equivalence class to correspond with the pitch class (in this example the durations used are absolute, but there are similar cases in which composers have proposed that durations in the ratio 1:2 be regarded as members of an equivalence class – a seemingly arbitrary proposition prompted by analogy with frequency), there is no analogue for inversion and transposition (the fact that, for instance, the pairs semiquaver/dotted quaver and crotchet/dotted crotchet have the same ‘duration interval’ is of dubious perceptibility) and the listener may easily miss the distinction between, for example, 11 and 12 demisemiquavers.
Babbitt has used rhythmic orderings which are formally analogous with pitch-class serialism. The first of the Three Compositions for Piano (1947) employs a four-element duration series: 5–1–4–2. This may be ‘inverted’ by complementation of the durations to six (complementation of pitch-class numbers to 12 is equivalent to inversion in pitch-class serialism), thus producing 1–5–2–4; the generation of R and IR forms is straightforward. In later works Babbitt’s rhythmic serialism is subtler. The analogue of pitch is now not duration but time point, defined as the duration which separates the attack from the beginning of the bar. For instance, it is possible to write a series analogous to ex.9 by interpreting pitch-class numbers as time-point numbers (ex.22). Duration is now equivalent to interval (and, as in the rhythmic serialism of Boulez and Berg, it may be filled in part by silence), but only consistently so if the bar contains an integral multiple of 12 units. Time-point series may be ‘inverted’ by complementation of their time-point numbers to 12; they may be ‘transposed’ by addition of a constant value to each time-point number; they may be retrograded; they may be associated by ‘combinatoriality’; and they may generate secondary and derived sets. The perceptibility of time-point serialism must remain questionable, however; in particular, it depends on the perception of metre, which may well be doubtful when several serial forms such as ex.22 are presented simultaneously.
If rhythmic serialism raises difficulties of perceptibility (and performability), these are still more acute when serial procedures are applied to other sound aspects (dynamics, tempo, timbre/attack/instrumentation etc.). In the early 1950s several European composers, notably Boulez, Stockhausen and Nono, adhered more or less firmly to such extensions of serialism; the term ‘total serialism’ was coined for these endeavours. Boulez’s Structures I contains not only the rhythmic serialism described above but also quasi-serial composition using sets of 12 dynamic markings and 12 indications of attack. The sort of heterogeneity that issued from such practices is illustrated in ex.23, from the opening of Stockhausen’s Kontra-Punkte (1952), though music constructed so consistently in isolated ‘points’ is rare in this composition and, indeed, in Stockhausen’s work as a whole. Note that the first five bars announce a 12-note set, but the pitch-class serialism of the work is far from orthodox.
Few compositions apart from Boulez’s Structures I attempt to follow ‘total serialism’ with any degree of thoroughness, but the notion did give rise to ideas that remained important in the work of those composers most closely associated with it, notably Boulez himself, Stockhausen, Nono and Pousseur. Principal among these ideas were the avoidance of repetition at all levels and in all domains, and the pre-compositional creation of ‘scales’ determining features that had not been so determined previously, even if the choice made from those ‘scales’ was not always in accordance with any serial procedure. Stockhausen’s Gruppen for three orchestras (1955–7) makes serial use of a ‘chromatic scale’ of 12 tempos, with an ‘octave’ between, say, crotchet = 60 and crotchet = 120, and the other values in a geometric progression analogous to that of the equal-tempered semitone scale. Again, the differentiation of degrees between vocal sound as sound and vocal sound as semantic meaning in Boulez’s Le marteau sans maître for voice and instruments (1953–5) and Stockhausen’s Gesang der Jünglinge for tape (1955–6) may be traced to the experience of ‘total serialism’.
Another aspect of ‘total serialism’ was the search for forms that would be in some way consonant with the method. Boulez’s Trope, mentioned above, shows this approach. Barraqué spoke of an immense, unfinished work, such as his La mort de Virgile, as being the consequence of serial procedures, perhaps specifically of his own concept of ‘proliferating series’. And the permutational nature of serial composition was one cause of the introduction of aleatory forms allowing the performer(s) to permute passages of composed music.
A few of the problems of perceptibility associated with the serialism of rhythmic elements and other non-pitch aspects have been alluded to, but the question of whether pitch-class serialism is perceptible has not yet been mooted. Meyer has raised doubts in this area on several grounds: early learning conditions the listener to the perception of tonal but not serial music; serial music is often composed with a very small degree of redundancy (i.e. listeners can miss only a very little of the information presented if they are to perceive serial procedures); different serial works, even by the same composer, may employ quite different serial procedures, so that learning to perceive those in one work may not help the listener in others; and finally, perception of serial procedures is not assisted by simple relationships, such as octaves, perfect 5ths and 1:2 duration ratios, which are, most commonly, specifically avoided. Lévi-Strauss has asserted that serial music cannot operate as a communicable language because it lacks a primary ‘level of articulation’ (provided in tonal music, for example, by the hierarchical relationships between pitch classes in the diatonic scale) necessary to establish and define the listener’s expectations. Ruwet has questioned the work of postwar European serial composers on these and other grounds, also from the standpoint of structural linguistics. It should be noted that these writers, with the possible exception of Lévi-Strauss, have not therefore condemned serial music, but have rather pointed out the difficulties that stand in the way of perceiving serial relations.
In replying, serial composers have usually taken one of three positions: that serial procedures are not to be perceived by the listener (Schoenberg’s injunctions against analysis need not be taken as implying concurrence with that view); that serial procedures are not perceived consciously, but the music gives an effect of coherence which the listener cannot explain; or that serial procedures can be perceived, given the listener’s cooperation in learning. This last attitude is implicit in the compositional methods and explicit in the written statements of Babbitt. The other positions raise a number of new questions. What is unconscious perception? If serial procedures cannot be perceived, do they give rise to relations which can be, and if so, what are those relations? Or is serial music perceived as incoherent, and if so, does that limit its capacity to communicate the composer’s thought?
It need not surprise us that serialism arose at a time when such questions of intentionality and communication began to become acute, and composers' uses of serialism should be considered as contributions to a debate rather than as decisive answers. Because its rules can be applied mechanically (Boulez's Structures Ia almost composed itself), serialism explores the boundaries between the automatic and the thought, the inevitable and the willed, the predetermined and the determined; it asks us to consider how much our way through music – whether as composers, performers, analysts or listeners – is guided by rules newly evidenced in the piece at hand, how much by instinct and tradition. The fact that the first works of Babbitt and Boulez were contemporary with the early practical development of computers is also suggestive. After the great wave of the 1950s, serialism became perhaps less forward in the minds of most composers, and discussions of method faded from the manifestos. However, serial principles of ordering and manipulation went on being practised by composers as diverse as Henze and Ferneyhough, and serialism's algorithmic character indicates a kinship with techniques that came into prominence later and might appear quite contrary, such as minimalism, and even with the imitation of historical styles and forms. However, serialism is also distinctive as the technique of choice for composers who feel or have felt themselves engaged in music as an evolving language, with a coherent history traceable back to Beethoven, Haydn or the Renaissance.
K. Stockhausen: ‘… wie die Zeit vergeht …’, Die Reihe, iii (1957), 13–42; repr. in Texte, i (Cologne, 1963); Eng. trans. in Die Reihe, iii (1959), 10–40
G. Ligeti: ‘Pierre Boulez: Entscheidung und Automatik in der Structure 1a’, Die Reihe, iv (1958), 38–63; Eng. trans. in Die Reihe, iv (1960), 36–62
N. Ruwet: ‘Von den Widersprüchen der seriellen Sprache’, Die Reihe, vi (1960), 59–70; Eng. trans. in Die Reihe, vi (1964), 65–76
P. Boulez: Musikdenken heute (Mainz, 1963; Fr. orig., Paris, 1964; Eng. trans., 1971)
K. Stockhausen: Texte (Cologne, 1963–89)
C. Lévi-Strauss: Le cru et le cuit (Paris, 1964; Eng. trans., 1970), 31ff
P. Boulez: Relevés d’apprenti (Paris, 1966; Eng. trans., 1991)
L.B. Meyer: Music, the Arts, and Ideas (Chicago and London, 1967)
H. Pousseur: Fragments théoriques I sur la musique expérimentale (Brussels, 1970)
U. Stürzbecher: Werkstattgespräche mit Komponisten (Cologne, 1971)
R. Maconie: The Works of Karlheinz Stockhausen (London, 1976, 2/1990)
P. Griffiths: Boulez (London, 1978)
H. Henck: Karlheinz Stockhausen's ‘Klavierstück X’: a Contribution toward Understanding Serial Technique (Cologne, 1980)
P. Boulez: Points de repère (Paris, 1981; Eng. trans., 1986)
J. Häusler, ed.: Pierre Boulez: eine Festschrift zum 60. Geburstag (Vienna, 1985)
W. Glock, ed.: Pierre Boulez: a Symposium (London, 1986)
S.. Dembski and J.N. Straus, eds.: Milton Babbit: Words about Music (Madison, WI, 1987)
J.-J. Nattiez, ed.: Pierre Boulez and John Cage: Correspondance et documents (Winterthur, 1990; Eng. trans., 1993)
L. Koblyakov: Pierre Boulez: a World of Harmony (Chur, 1990)
H. Conen: Formel-Komposition: zu Karlheinz Stockhausens Musik der siebziger Jahre (Mainz, 1991)
C. von Blumröder: Die Grundlegung der Musik Karlheinz Stockhausens (Stuttgart, 1992)
Jean Barraqué, Musik-Konzepte, no.82 (1993)
D. and J.-Y. Bosseur: Révolutions musicales: la musique contemporaine depuis 1945 (Paris, 1993)
A. Mead: An Introduction to the Music of Milton Babbitt (Princeton, NJ, 1994)
J. Rahn, ed.: Perspectives on Musical Aesthetics (New York, 1994)
J. Boros and R. Toop, eds.: Brian Ferneyhough: Collected Writings (Amsterdam, 1995)
P. Griffiths: Modern Music and After (Oxford, 1995)
For further bibliography see Twelve-note composition.