
Anonymous 9th-century Latin music treatises of signal importance for the early history of modal theory and of polyphony. They are generally transmitted together in the manuscript tradition, frequently with other contemporary tracts (ed. in Schmid, 1981) but most of all with Boethius’s De institutione musica. Though best known for containing the earliest extant discussions of (improvised) polyphonic singing (organum), they are equally notable for transmitting the first chant melodies preserved in a precise pitch notation and for drawing upon a wide range of late Latin literary and philosophical sources; they thus document the intellectual environment as well as the state of musical theory and practice of the Carolingian Renaissance. Although the origins of the treatises are still wrapped in mystery, major advances in the understanding of Musica enchiriadis and Scolica enchiriadis have been possible following the completion of Schmid’s critical edition (1981), the dissertation by Phillips (1985) and the first complete published translation of both treatises (Erickson, 1995) since Schlect’s German translation (1874–6) based on Gerbert’s edition of 1784. (Unless otherwise stated, the edition and translation of Musica enchiriadis and Scolica enchiriadis referred to in this article are those by Schmid, 1981, and Erickson, 1995.)
2. Sources, dating, authorship, dissemination.
3. The dasian scale and notation.
5. Theory and practice of organum.
RAYMOND ERICKSON
Musica enchiriadis, Scolica enchiriadis
Musica enchiriadis [ME], which has no title in the earliest sources, is a succinct, well-argued account of the theory and practice of ecclesiastical music of the time. The first nine of its 19 chapters are concerned with monophonic chant, a notational system for representing melodies (dasian notation), a description of the modes based on both final and ambitus (but not of modal octave species), vocal exercises for practising different modal characteristics (determined by the placement of the semitone), and basic musical and mathematical terminology. Chapters 10–18 take up the ‘symphonies’ (consonances of octave, 5th and 4th) and their use in simultaneous (in unum) singing, whether in octave doublings or in improvised polyphony (diaphonia, organum) in which the chant is generally replicated at the 4th or consistently replicated throughout at the 5th, with octave doublings possible in both cases. Chapter 18 closes with philosophical musings concerning the mysterious fact that some tones when combined produce harmony and others do not, that ‘the same principle that controls the concord of pitches regulates the natures of mortals’ and that the harmony of the world is due to the mathematical relationships that regulate and unite all things in it. Chapter 19, which addresses essentially the same issues in different terms, notably by an interpretation of the Orpheus myth in a unique version largely based on Fulgentius, could therefore be considered as superfluous and may well be the misplaced prologue to Scolica enchiriadis [SE], to which it apparently refers in a concluding reference to ‘the little work following’ (Phillips, 1985).
SE, on the other hand, is a dialogue in three unequal parts, the total being three times as long as ME. Its title, probably original, may have been modelled on the rhetorical treatise in dialogue form of Fortunatianus (see Spitta, 1889; Phillips, 1985) entitled Scolica (i.e. ‘excerpts’) enchiriadis (possibly a corruption of the Greek encheiridios, ‘handbook’). Part i defines music in Augustinian terms as ‘bene modulandi scientia’ and states that the skilled or learned singer (cantor peritus) must know the properties of the individual pitches, the rhythmical aspects of chant performance, and other things beyond these (extrinsecus occurrentibus) that are never clearly defined but might refer to polyphony or possibly (as one 11th-century gloss suggests) even singing ability (bona vox). In addition to describing piecemeal the dasian pitch set of 18 notes and their correlative symbols and tetrachords, SE discusses at length common errors in singing chants, caused by misplacing the semitone in a melody, all of which are represented graphically as well as in words. These examples also emphasize the pentachordal structure characteristic of the dasian system (which also produces modal identity at that interval). Part i closes with a discussion of how chants may be adorned by varying the lengths of notes; the description is not precise but does indicate that the ratio of long to short notes is 2:1, that lengthening of notes would be especially appropriate at the ends of phrases and verses, and that entire text units (such as a psalm verse) could be doubled or halved in tempo. Nonetheless, the oldest manuscripts are lacking clearly legible examples, so any reconstruction of the illustrations is speculative.
Part ii of SE is itself subdivided into (1) a discussion of the symphonies and organal singing, and (2) an introduction to quadrivial thinking which asserts the importance of number and mathematics for music and which adduces an extended passage from Augustine’s De ordine (ii.4f) to underscore how number is the foundation of all the disciplines of the quadrivium. This discussion prepares the way for part iii, which is almost as large as the previous two parts combined and consists primarily of a systematic but selective account of number theory drawn mainly from Boethius and Cassiodorus. Topics include definitions of numerical and spatial (continuous) quantity (multitude and magnitude, respectively) and how ‘in likeness to both kinds of quantity, arithmetic brings forth out of itself music’ so that ‘when the differences of pitches are based on quantity in this way, the pitches sound together in a sweet mixture according to the contrary natures of the two types of quantity’ (Schmid, 116.12f; Erickson, 70). Moreover, because music treats non-movable quantities not in terms of themselves (per se) but in relation to other such quantities (ad alium), an investigation of inequalities is necessary. There thus follows a detailed exposition of types of inequality (multiple, superparticular, superpartient, multiple superparticular, multiple superpartient) and why only two types of inequality – multiple and superparticular – are suitable for music. The intervals of music are matched with multiple (i.e. duple – 2:1, triple – 3:1, quadruple – 4:1) or superparticular (sesquialter – 3:2, sesquitertian – 4:3, sesquioctaval – 9:8) ratios. Then, beginning from the integer 192 and using these ratios as multipliers, an octave scale is constructed with the resulting numbers 192 216 243 256 288 324 364½ 384 representing the pitches (Schmid, 142.477–144.510, 145.descr.4; Erickson, 86f, fig.43). Although uncommented upon, this series is not congruent with any pair of tetrachords in the dasian system but matches rather the modern C major scale, which is the basis for most of the diagrams in part iii, and is possibly connected with the scale given by Hucbald that he associates with the organ (GerbertS, i, 110b–111a). There then follows a monochord division to produce the same scale. Finally, in the treatise’s closing paragraphs, the discussion reverts to the different intervallic arrangements of tetrachords and their relationship to the modes by the placement of the semitone, reasserting that, in the dasian scale, modal identity is to be found at the 5th degree but not at the 8th. This means that when an octave consonance is desired with a given tone in the scale, the octave must be made perfect, even if this means going outside the pitches of the dasian scale. The treatise closes non-climactically with the statement that such application of the duple proportion ‘both preserves the symphony [of the octave] and retains the category of trope [i.e. mode]’ in the two voices.
Musica enchiriadis, Scolica enchiriadis
If the number of extant sources (46 listed in Schmid, 1981; plus one more described by Lochner, 1988) is any indication, the Enchiriadis treatises must be considered among the most widely read musico-theoretic texts of the Middle Ages. Only Boethius’s De institutione musica, the dialogue attributed to Odo (see Odo, §3), and Guido of Arezzo’s Micrologus survive in more sources than ME and SE. Moreover, other medieval treatises much valued today, such as Hucbald’s De harmonica institutione, had very little currency in the Middle Ages, whereas Guido of Arezzo, Berno of Reichenau, Hermannus Contractus, and the author of the Quaestiones in musica all draw on (or criticize) the terminology and teachings of ME and SE.
Regarding the origins of ME and SE, recent research suggests that the oldest extant source, D-DÜl H 3, may have been copied from the non-extant original of SE. Surviving only as a fragment, D-DÜl H 3 was most likely written at the Benedictine abbey of Werden (near Essen) in the last years of the 9th century, possibly during the rule of Abbot Hoger (d 906), to whom authorship is ascribed in some of the earliest sources (see Torkewitz, 1997, and 1999). The oldest more or less complete source of both treatises, from 10th-century St Amand, is F-VAL 337. There are also five later sources that transmit the so-called Inchiriadon (ed. in Schmid, 1981), a compilation of an apparently earlier version of part of ME mixed with aspects more advanced than ME. More primitive in this work is the less technical and less sophisticated use of Boethius’s De institutione musica than that found in ME (see Duchez, 1980); more advanced is the incorporation into its modal theory of the notion of modal octave species and, associated with them, the Greek tribal names Dorian, Phrygian, Lydian and Mixolydian (Schmid, 204.462–4), although the last name occurs only in the associated diagram and not the text (204.descr.14). In any event, the complete texts of ME and SE as they are found in the early sources are probably not in their original form: as mentioned above (§1) chapter 19 of ME would serve more appropriately as an introduction to SE; nothing prepares the reader in the opening passages of SE for the enormous emphasis on number theory that dominates more than half of the treatise; and as a practical handbook, part i and the first half of part ii can be seen as roughly equivalent to ME and satisfy quite adequately the practical information needed by the ‘skilled singer’. These and other features suggest that both ME and SE have complicated histories involving several stages of evolution – of addition, replacement and of shuffling of materials – ultimately resulting in the texts that have been transmitted. It is therefore possible that at least parts of the texts date from the first half of the 9th century; but it also seems likely that the standard versions of ME and SE known today are from much later in the century.
Specific similarities in content (dasian notation, discussion of organum etc.), as well as dissimilarities to other treatises of roughly the same period (Aurelian of Réôme, Hucbald of St Amand), clearly suggest that ME and SE came from the same intellectual and musical environment. However, there are also indications that ME and SE did not have the same authors. (It is also possible that both had more than one author, and that, especially in the case of SE, a compiler rather than an author might have played some role.) Sometimes this is revealed in small differences in locution: ME refers to ‘the tetrachord of the graves [notes]’ but SE to ‘the grave tetrachord’; similarly, neuma regularis in SE is simply neuma in ME. Sometimes there are more substantial differences: a change of locus for the organal voice when the chant melody has a wide range is discussed in ME (chap.18) but not in SE. Moreover, the term ‘organum’ is not used identically in both: whereas both use it to designate the organal voice, only ME equates it with the two-voice musical texture also called diaphonia. Finally, ME’s author (chap.16) is very aware of the necessity of justifying the 11th as a consonance (as does Ptolemy, Harmonics, i.6, translated by Boethius, De institutione musica, v.9) to rationalize octave doublings of organum at the 4th, but SE presents the 11th (in different places) variously as a consonance and as a dissonance and lays great stress on the principle of commensurality or connumerality (Schmid, 109.198f, pp.125–8, passim; Erickson, 67, 76–8), which does not apply to the ratio 8:3 (the 11th). Thus the theoretical justification for octave doubling of organum at the 4th illustrated elsewhere in SE is undermined (Schmid, 96.descr. and 100.descr.36; Erickson, 59, figs.32 and 62, fig.36). This inconsistency contrasts markedly with ME, which strongly argues that the 11th is a consonance.
Musica enchiriadis, Scolica enchiriadis
One of the most characteristic features of ME and SE is the use of a notation that is found only in a small number of theoretical writings (a rare, partial use in a practical source occurs in F-Pn 9488; see Santosuosso, 1989, p.35); it is one of the few precise pitch notations used before the development of the staff in the second half of the 11th century. Therefore, the melodies represented by this notation – mostly from the Office Hours and none from the Mass – in the Enchiriadis treatises are among the oldest examples of melodies whose precise pitch content is known. (See Notation, §III, 1(v)(a).)
Dasian notation is so called because it is based on the use of the Greek grammatical accent for rough breathing known as the daseia: ‘. By combining it with the letters ‘C’ and ‘S’ and rotating the symbols (notae, figurae, karacteres) in various ways, the symbols for the 1st, 2nd and 4th pitches (protus, deuterus, tetrardus) of each tetrachord are generated; the 3rd pitch (tritus), which marks the semitone – ‘the very heart and soul of music’ (Schmid, 151.590f; Erickson, 90) – has an anomalous set of signs to signal its distinctiveness. The entire scale of 18 pitches, made up of four named tetrachords and two additional pitches ‘added at the top’ is illustrated in ex.1. Although the authors of ME and SE both refer to the ‘dasia’ in connection with the notation, presumably because of the familiarity with the grammatical sign, the same graphic form is also a note form of Greek vocal notation transmitted by Boethius in his De institutione musica (iv.3).

Although this arrangement has elements in common with ancient Greek theory (tetrachords, 18 pitches etc.), it is different from all other tetrachord-based systems. Generations of scholars have been puzzled by the inconsistency of intervals at the 4th and especially 8th degree, since ME and SE both discuss octave doublings and (essentially) parallel organum at the 4th. It is possible that the pitch series actually corresponds to the melodic content of 9th-century melodies, which were later modified when an octave-based modal theory was imposed on the chant repertory (see Phillips, 1985).
Musica enchiriadis, Scolica enchiriadis
The eight ‘modes’ or ‘tones’ (cf Atkinson, 1987) are described in the Enchiriadis treatises with greater precision than in Aurelian’s (presumably) earlier Musica disciplina (c840), using both final and ambitus as criteria. Each mode has an authentic and plagal form, sharing a final but having different ranges: the lower boundary for both is said to be the 5th below the final, while the upper boundaries are a 9th and a 5th above the final for authentic and plagal modes respectively.
SE also recognizes that transposition at the 5th degree does not change the mode. Tones a 5th apart have the same name, hence the same function; therefore, SE asserts, they are ‘concordant with each other because of a certain natural kinship [socialitas]’ (Schmid, 73.161f; Erickson, 43); however, tones a 4th away (compares, ‘compeers’; Schmid, 82.320; Erickson, 48) are also said to enjoy a similar relationship (although the term compar is also used for a note a 5th away; Schmid, 173.159, Erickson, 42). SE also finds these notes ‘associated with the final’ used as the last notes of phrases (comma, colon; Schmid, 82.321–3, Erickson, 48f).
The modes in ME/SE are named from their finals and qualified by their ranges, e.g. protus authentus, protus plagis, although other terms are used (e.g. minor, subiugalis and lateralis for plagal). The tribal names Dorian, Phrygian, and Lydian (a trio that frequently appears in Greek music theory as well as in Boethius) also occur (in ME only), but they are not associated with specific modes until the Alia musica and, as mentioned above, Inchiriadon.
Musica enchiriadis, Scolica enchiriadis
Although a discussion of singing in parts was new in the theoretical literature, the practice was apparently not a novelty when the Enchiriadis treatises were written: ME refers to it as ‘diaphony, that is, two-voiced song, or, customarily, organum’; SE does not, in fact, give this practice a name. (However, in both treatises organum is a term for the organal voice.) Organum properly refers to singing in 4ths and 5ths. In the Enchiriadis treatises, the organal voice (vox organalis) is below the principal voice (vox principalis) in a basic two-voice texture.
Within
the dasian system complete parallelism is possible in organum at the 5th (ex.2), but not at the 4th (ex.3), because the interval between a deuterus pitch and the
tritus below it is a tritone, not a perfect 4th, thus prohibiting the organal
voice moving below tetrardus, especially at the beginnings and endings of
phrases. In ex.3, therefore, the two voices begin in unison to avoid the
tritone E–B![]() that would
occur on the third and last syllables. According to SE: ‘at the symphony
of the diatessaron an organal voice does not so simply and consistently
accompany a principal voice as at the diapente but, by some natural law of its
own, it stands still in certain places and is not able to proceed further
consonantly’ (Schmid, 102.87–90, Erickson, 61).
that would
occur on the third and last syllables. According to SE: ‘at the symphony
of the diatessaron an organal voice does not so simply and consistently
accompany a principal voice as at the diapente but, by some natural law of its
own, it stands still in certain places and is not able to proceed further
consonantly’ (Schmid, 102.87–90, Erickson, 61).
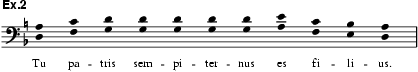

In chapter 18 of ME, it is further shown that when the chant melody shifts into different tetrachords it may be necessary for the organal voice to do likewise, the new lower limit being the tetrardus of the new tetrachord (ex.4).

Octave doubling is not regarded as organum, but rather as a natural phenomenon produced, for example, when men and boys sing the same melody. Although octave, 5th and 4th are all considered ‘symphonies’ (Schmid, 23.6–8; Erickson, 13), the octave is singled out as an equisonus (‘equal-sounding’) interval, ‘for in this symphony a pitch is revealed anew’ (Schmid, 26.27f; Erickson, 15). Nonetheless, octaves may be employed in the performance of plainchant or of organum. In organum, principal and organal voices are subject to octave doubling both above and below such that each voice could sound in three octaves, the highest being sung by boys; SE even gives examples of doublings at one or two octaves above the basic organal voice, which itself, however, is omitted, suggesting that virtually any combination of up to six parts might be employed (Schmid, 96.descr.6 and 101.descr.11; Erickson, 59, figs.32 and 63, fig.37). Moreover, the use of instruments was also apparently sanctioned: ‘For human voices can be mixed with one another and with some musical instruments, not only two and two but also three and three’ (Schmid, 40.10–12; Erickson, 22).
It should be noted that in the manuscript sources examples illustrating organal practice more often than not dispense with dasian notation for voices other than the chant melody; the notation was designed to represent the plainchant melodies only and is therefore generally incapable of representing all the pitches used in an organal performance, especially at the 4th and/or with octave doublings. Nowhere in the treatises is it suggested that the notation was invented to accommodate multi-voice textures.
Musica enchiriadis, Scolica enchiriadis
One of the most interesting and impressive aspects of the Enchiriadis treatises, distinguishing them from all other medieval writings on music theory, is the wide range of classical, patristic and other late Latin sources that they draw upon. There are terminological borrowings, direct quotations and/or paraphrases of passages from Virgil’s Aeneid, Censorinus’s De die natali, Calcidius’s translation and commentary on Plato’s Timaeus, Augustine’s De musica and De ordine, St Jerome’s Vulgate (Romans), Boethius’s De arithmetica, De institutione musica, and Consolatio philosophiae, and Cassiodorus’s Institutiones. By far the most influential author is Boethius, not only in terms of the number of works utilized but as regards the extent of the borrowings. Boethius’s name is also invoked more than any other author; he is referred to as the ‘doctor magnificus’ (Schmid, 44.11; Erickson, 25) and ‘praestantissimus auctor’ (Schmid, 59.39; Erickson, 32; see also Cohen, ‘Metaphysics’, 1993). Second in importance is Augustine (a direct source for SE only), whose De musica probably provides a model for the dialogue form and opening of SE and also for the brief discussion of rhythm found at the end of part i SE, and whose reflections on the origin of the various arts and disciplines in De ordine is quoted at some length in part ii. Cassiodorus also figures prominently as a source for the introduction to quadrivial studies in SE, part ii, and in the discussion of inequality in part iii, although mixed in with Boethian and other materials.
The name of the 9th-century philosopher Johannes Scottus Eriugena has, since the time of Coussemaker, been associated with ME. Although certain Neoplatonic elements in both ME and SE have been attributed to Scottus (Phillips, 1985), there is really no direct evidence that he influenced or was influenced by the two treatises; in fact the Neoplatonic and neo-Pythagorean aspects can be shown to have a more likely origin in Boethius (Erickson, 1992).
Musica enchiriadis, Scolica enchiriadis
ME and SE contain many features that recall Aurelian’s presumably earlier tract Musica disciplina and which may well reflect Byzantine-Frankish contacts in the 8th and 9th centuries: eight categories of mode (suggestive of but not identical with the Byzantine oktōēchoi) divided into two groups of four, although the modes themselves are different; a basic scale system made up of tetrachords; the Greek-derived terms protus, deuterus, tritus, tetrardus; the noenoeane formulas (used in ME and SE to exemplify different modes) that recall the Byzantine enēchēmata.
Musica enchiriadis, Scolica enchiriadis
CoussemakerS, ii, 74–8
GerbertS, i, 152–212
R. Schlect, trans.: ‘Musica enchiriadis von Hucbald’, MMg, vi (1874), 163–91; vii (1875), 1–93; viii (1876), 89–101
H. Schmid, ed.: Musica et scolica enchiriadis, una cum aliquibus tractatulis adjunctis (Munich, 1981)
R. Erickson, trans.: Musica enchiriadis and Scolica enchiriadis, ed. C.V. Palisca (New Haven, CT, 1995) [Eng. trans.; incl. introduction and notes]
D. Torkewitz, ed. and trans.: Das älteste Dokument zur Entstehung der abendländischen Mehrstimmigkeit (Stuttgart, 1999)
Musica enchiriadis, Scolica enchiriadis
Grove6 (L.E. Gushee)
MGG2 (N. Phillips)
H. Müller: Hucbalds echte und unechte Schriften über Musik (Leipzig, 1884)
P. Spitta: ‘Die Musica enchiriadis und ihre Zeitalter’, VMw, v (1889), 443–82
R. Steglich: Die Quaestiones in musica (Leipzig, 1911/R)
J. Handschin: ‘Die Musikanschauung des Johannes Scottus (Erigena)’, Vierteljahrsschrift für Literaturwissenschaft und Geisteswissenschaft, v (1927), 316–41
H. Sowa: ‘Textvarianten zur Musica Enchiriadis’, ZMw, xvii (1935), 194–207
W. Wiora: ‘Das vermeintliche Zeugnis des Johannes Eriugena für die Anfänge der abendländischen Mehrstimmigkeit’, AcM, xliii (1971), 33–43
F. Reckow: ‘Organum’ (1972), HMT
L.A. Gushee: ‘Questions of Genre in Medieval Treatises on Music’, Gattungen der Musik in Einzeldarstellungen: Gedenkschrift Leo Schrade, ed. W. Arlt and others (Berne, 1973), 365–433
E.L. Waeltner: Die Lehre von Organum bis zur Mitte des 11. Jahrhunderts (Tutzing, 1975)
M. Bielitz: Musik und Grammatik: Studien zur mittelalterlichen Musiktheorie (Munich, 1977)
E.L. Waeltner: Organicum melos: zur Musikanschauung des Johannes Scottus (Eriugena) (Munich, 1977)
M.-E. Duchez: ‘Jean Scot Erigène premier lecteur du De institutione musica de Boèce?’, Eriugena: Studien zu seinen Quellen: Freiburg 1979, ed. W. Beierwaltes (Heidelberg, 1980), 165–87
M. Huglo and N. Phillips: ’The Versus Rex caeli: Another Look at the So-Called Archaic Sequence’, JPMMS, v (1982), 36–43
N. Phillips: ‘The Dasia Notation and its Manuscript Tradition’, Musicologie médiévale: Paris 1982, 157–73
N.C. Phillips: Musica and Scolica enchiriadis: the Literary, Theoretical, and Musical Sources (Ann Arbor, 1985)
N. Phillips and M. Huglo: ‘Le De musica de Saint Augustin et l’organisation de la durée musicale du IXe au XIIe siècles’, Recherches augustiniennes, xx (1985), 117–31
C.M. Atkinson: ‘Harmonia and the Modi, quos abusive tonos dicimus’, IMSCR XIV: Bologna 1987, iii, 485–500
F. Lochner: ‘Un manuscrit du théorie musicale provenant d’Echternach: Luxembourg, B.N. MS I:21’, Scriptorium, xlii (1988), 256–61
A.C. Santosuosso: Letter Notations in the Middle Ages (Ottawa, 1989)
H. Schmid: ‘Zur sogenannten Pariser Bearbeitung der Musica enchiriadis’, Tradition und Wertung: Festschrift für Franz Brunhölzl, ed. G. Bernt, F. Radle and G. Silagi (Sigmaringen, 1989), 211–18
N. Phillips: ‘Classical and Late Latin Sources for Ninth-Century Treatises on Music’, Music Theory and its Sources: Antiquity and the Middle Ages, ed. A. Barbera (Notre Dame, IN, 1990), 100–35
R. Erickson: ‘Boethius, Eriugena, and the Neoplatonism of Musica and Scolica enchiriadis’, Musical Humanism and its Legacy: Essays in Honor of Claude V. Palisca, ed. N.K. Baker and B.R. Hanning (Stuyvesant, NY, 1992), 53–78
D.E. Cohen: Boethius and the Enchiriadis Theory: the Metaphysics of Consonance and the Concept of Organum (diss., Brandeis U., 1993)
D.E. Cohen: ‘Metaphysics, Ideology, Discipline: Consonance, Dissonance and the Foundations of Western Polyphony’, Theoria, vii (1993), 1–85
D. Torkewitz: ‘Zur Entstehung der Musica und Scholica Enchiriadis’, AcM, lxix (1997), 156–81
M. Haas: ‘Die Musica enchiriadis und ihr Umfeld: elementare Musiklehre als Propaedeutik zur Philosophie’, Musik und die Geschichte der Philosophie und Naturwissenschaften im Mittelalter: Fragen zur Wechselwirkung von “musica” und “philosophia” im Mittelalter, ed. F. Hentschel (Leiden, 1998)
M. Walter: ‘Vom Beginn der Musiktheorie und dem Ende der Musik: über die Aktualität des Mittelalters in der Musikgeschichte’, AcM, lxx (1998), 209–29