Change ringing.

An art of bellringing peculiarly English and producing a music of its own. It was developed in England during the 17th century, while on the Continent there was a parallel, although unconnected development in the carillon.

1. History.

2. Methods of change ringing.

WILFRID G. WILSON/STEVE COLEMAN

Change ringing

1. History.

For centuries before the development of change ringing, the general shape and form of the bell and the uses of bellringing had been established. Probably the most characteristic sound in the medieval town was that of the chiming of bells, announcing the time for prayer or simply the hour. The bells were chimed, singly or in twos or threes, by means of a rope and lever which enabled them to be swung just far enough for the clappers to strike them. They were hung in church towers because such buildings were almost the only ones large enough to contain them.

Change ringing in approximately the form we now know it began around the end of the 16th century and expanded considerably, both in popularity and complexity, during the second half of the 17th century. The adoption of change ringing as a pastime by associations of well-to-do young men in the middle of the 17th century was particularly influential in its development, although its strength has always been as a vernacular folk art. The growth of ringing is discussed by Sanderson.

One of the changes brought about by the Reformation in England and the simplification of public worship and, in the 17th century, the Puritan tenet of sabbatarianism, was the almost complete secularization of change ringing. The quasi-liturgical ringing of bells was forbidden, although of course the ban was never completely successful, and change ringing remained a secular hobby to be carried out on any day of the week except Sunday; indeed it was abhorred by most of the clergy.

After a period of stagnation in the first half of the 19th century, there was a movement in the second half for reform in the use of bells for church purposes, taking its seeds from the Oxford Movement. Associations were formed throughout the country based on county or diocesan areas, and they encouraged the use of bells to call people to worship and to mark the great church festivals. Change ringing was advocated as an element in supporting this reform. The secular side of ringing still remained, but to ring the bells regularly on Sundays became the overriding duty of ringers.

Change ringing is once again flourishing, with local associations covering the whole of the British Isles. The number of active ringers remained fairly constant throughout the 20th century at between 35,000 and 40,000, but it increased to over 50,000 by the year 2000 in a drive to ring every bell in the country at the start of the new millennium. There is also a rapidly growing, although limited amount of change ringing in other parts of the world, particularly in North America and Australia but also in New Zealand and southern Africa. The organization unit is the ‘local band’ (the group of ringers attached to a particular ‘ring’ of bells) and it is this strong local structure which has enabled change ringing to flourish continuously for 400 years. Some of the early pieces of ringing (‘methods’) are rung as much today as they were 350 years ago, but since World War II there has been rapid growth in extremely complex methods, which the ringers of earlier periods would have thought impossible to cope with.

Change ringing

2. Methods of change ringing.

Fig.1 shows the way in which a modern bell is hung for the purpose of change ringing. The crown of the bell is firmly bolted to the headstock, which revolves on ‘gudgeons’ working in ball-bearings. To the headstock is fixed a large wooden wheel, flanged to hold the rope which passes down, by means of pulleys and guides, into an approximate circle with its neighbours in the ringing-room, normally 9 metres or more below. Here the ringer pulling on a ‘sally’ (a coloured woollen section woven into the rope about 240 cm from the end) sets the bell in motion (fig.2), making it swing alternately in opposite directions, one double swing for each pull. When the swing of the bell exceeds 90° from the vertical, the garter hole passes a stationary pulley (concealed behind the front left corner of the frame in fig.1) and the direction in which the rope leaves the garter hole is reversed. The clapper strikes within each swing when the bell is approaching the end of its arc. With each pull the bell describes an ever increasing arc until it is mouth upwards; the process of getting the bell into this position is called ‘raising’, and the bell when raised is said to be ‘up’. The bell may, if desired, be allowed to go a little way over the ‘balance’ point and be held there. If allowed to go even further until the stay rests against the slider, it is said to be ‘stood’ or ‘set’ and can be left that way during rest periods. This process of ‘full circle’ ringing, with the facility of being able to hold the bell just over the balance point, enables the striking of the bell to be slightly delayed or advanced through small variations in pull so as to fit in with the other bells either in a repeated sequence or in changing patterns.

The starting point for all change ringing is the repeated ringing of all the bells in sequence down the musical scale (‘rounds’), most ‘rings’ of bells being tuned so that their strike notes are in a major key. (For a discussion of the tuning of bells see Bell (i), §2.) Normally there are six or eight bells in a ring although there may be fewer or more, with 16 the current maximum. In ringing rounds and in all change ringing it is considered essential that all bells are invariably struck in an even spacing one from another with the exception of a double interval at the end of every other change. No variation from this strict rhythm is permitted and achieving it is known as ‘good striking’. It is difficult because of the varying size of change ringing bells – the average weight being around 250 kg but some bells weighing up to four tonnes – and the remote and cumbersome nature of the equipment. Indeed, a bell hung for change ringing sounds two seconds after the physical action.

The earliest and simplest form of change ringing is known as ringing ‘call changes’. In this method the order of striking is varied from simple rounds by pairs of bells swapping their places at suitable intervals on the instructions of one of the ringers (called the conductor). Call change ringing is still practised throughout Britain and is especially used to give beginners practice in bell control. From this it is a short step to ringing simple methods.

The total number of changes possible on any number of bells (that is, the different sequences which can be obtained without repetition) is the factorial of the number: the number of permutations obtainable on three bells is factorial three, i.e. 3 × 2 × 1, or six changes; on four bells 4 × 3 × 2 × 1, or 24 changes; on eight bells 40,320 changes are possible, and on ten bells 3,628,800.

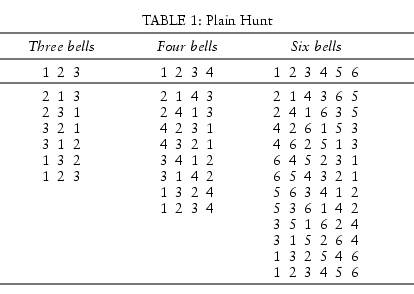
The basic principle involved in ringing changes on any number of bells is called ‘plain hunt’, the word ‘hunt’ being used in the sense of a course, or path among the other bells. Each bell is represented on paper by an ordinal, starting with 1 for the treble (the smallest bell) and going down the scale to the tenor (the largest bell). Table 1 shows examples of plain hunt on three, four and six bells. Each bell follows a regular path among the others, going from the front (or lead) up to the back (or behind) and then down to lead again. In each of the sets of changes given in Table 1, a line can be drawn along the path of any of the numbers, each representing a bell; the result will be a straight path from front to back and then from back to front, or vice versa. This progress of a bell is called plain hunting, and plain hunt produces twice as many changes as there are bells, each bell being struck twice in each position in the row: once on the way up and once on the way down.

These changes can be written out by reversing the order of the bells in pairs of adjacent numbers. In the six-bell example the second row is obtained by reversing the order of each of the three pairs; the next row by changing only the inner two pairs; and so on until the original order returns.

But change ringing is not confined to plain hunting. On three bells plain hunt produces all of the six possible changes. But on four bells only eight of the 24 possible sequences can be produced by plain hunt, and it is an essential tradition of change ringing to ring as many different changes as are possible in the time available without repetition. Plain hunting must therefore be varied to obtain more of the possible changes.

There are two main types of method: one for use with an even number of changing bells, the other with an odd number. In the latter, an even number of bells are rung but the tenor is always rung at the end of each change (‘ringing tenor behind’ or ‘covering’), with only the other bells changing. Each method of obtaining changes is described by its name and by the number of bells changing: even-bell methods are ‘minimus’ on four bells, ‘minor’ on six, ‘major’ on eight, ‘royal’ on ten and ‘maximus’ on twelve. Odd-bell methods are ‘doubles’ on five bells, ‘triples’ on seven, ‘caters’ (from quatres) on nine and ‘cinques’ on eleven. (In doubles two pairs of bells interchange at every permutation; in triples three pairs interchange and in caters four pairs interchange.) These descriptions have survived from the early days of change ringing.

The simplest of the even-bell methods, and the one best suited for use as an introduction to the inexhaustible complexities of change ringing, is Plain Bob. Its basis is the plain hunt, varied in the simplest way possible to produce more and different changes. On four bells plain hunt starts from rounds and returns to rounds in eight changes. This length, from the time the treble leads until it returns to lead again, is called a ‘lead’. At the first lead end (see Table 2) the bells are prevented from coming round (back to 1 2 3 4): the bell striking over the treble (3) stays in ‘seconds place’ (the second position) for another blow (called ‘making seconds place’). To prevent repetition the bells in thirds and fourths place (2 and 4 in Table 2) change places – this is called a ‘dodge’ – and a new row (1 3 4 2) is produced.

A second lead is then produced by plain hunting until its end is reached. A corresponding dodge is made and the row 1 4 2 3 is produced. The third lead, incorporating the same dodge when the lead end is reached, produces rounds. Thus all of the 24 possible changes on four bells have been rung, with no repetition and no omission. A line drawn through any one of the numbers 2, 3 or 4 in Table 2 will show the path of one bell in this ‘plain course’ of Plain Bob Minimus. Each of these ‘working’ bells has followed a path consisting of plain hunting, varied at the lead ends by making seconds place, a 3–4 dodge after the two blows behind (this is called 3–4 down) or a 3–4 dodge before the two blows behind (called 3–4 up). The treble has retained its plain hunting path throughout. When this Plain Bob method is rung on six bells a plain course of 60 changes is obtained by ringing five leads of plain hunt, each one incorporating a similar variation at the treble lead end. The lead ends starting from rounds for Plain Bob Minor are shown in Table 3.

Changes can now be rung, all different, for about two minutes, depending on the weight of the bells (which governs the speed of the ringing). The next stage is to vary the Plain Bob method further, introducing different changes until all the 720 changes possible on six bells can be produced. At the appropriate stage in the ringing, just before the treble leads, the conductor may call ‘bob’. This is an instruction to the ringers, or some of them, to alter their paths, thus producing a new row from which further changes can be rung. The variation made by a bob called at the last lead end of a plain course of Plain Bob Minor is shown in Table 4.

The difference caused by the bob is that instead of a bell making seconds place at the lead end, another bell makes fourths place. The effect is to alter the paths of three of the bells; consequently if a bob is called at the corresponding position twice more – that is at the 118th and the 178th changes – these bobs will affect the same three bells, and all six bells will be back at rounds in 180 changes.

If bobs are called at appropriate places it is possible to produce 360 changes – half the total number possible on six bells – but for complex mathematical reasons, it is not possible to obtain the full 720 changes in this method by bobs alone. The order of one pair of bells alone must be changed at one time if all or some of the other 360 changes are to be produced, and a further single change is then required to get back to rounds. To do this the conductor calls ‘single’ at the appropriate places. The effect is compared in Table 4 with a plain lead and a bob lead.

However many bells Plain Bob is rung on, the bobs and singles will affect only the bells which are in seconds, thirds or fourths place at the lead end. All the other bells follow the normal path as at a plain lead. But the number of positions at which bobs and singles may be called and made, and the number of changes they will produce become much greater on the higher numbers of bells. The most a normal ringer ever rings at one time without stopping is about 5000 changes, starting from and ending with rounds, and without repetition in between – although for doubles and minor where the total possible changes are less than 5000, periodic repetition is allowed. This length is called a ‘peal’ and takes about three hours to ring. ‘Quarter-peals’ (being about 1250 changes) are rung far more frequently than peals but the normal length rung on Sundays and for practice is a ‘touch’ lasting five to ten minutes, although many such touches are rung in a standard ringing session of between 30 minutes and two hours. The composer – whether of peals, quarter-peals or touches – must ensure that his compositions are ‘true’ (i.e. they contain no repeated changes) and that they are as musical as possible. A composition which is not true is said to be ‘false’.

Many ringers, and probably still more listeners, prefer the more obvious rhythmic and musical effect produced when the tenor bell is rung at the end of every row while the other bells change. On the normal ring of six or eight bells this means that an odd number of bells change. One of the earliest, but most lastingly popular, of the odd-bell methods is ‘Grandsire’. In the ringing (and as usually taught) it seems to be completely different from Plain Bob, but it is in fact a very simple extension of it. While Plain Bob on four bells consists of a plain hunting treble and three working bells, in Grandsire Doubles (i.e. on five bells) another bell does a plain hunt parallel to the treble. The lead of each in Table 5 shows only the plain hunt bells.

This double hunting path means that it is not possible for one of the working bells to make seconds place at the lead end, because all the working bells must keep out of the way of the hunting path of the treble and the ‘bell in the hunt’ (bell no.2 in Table 5); but, when 1 and 2 change over at the front, a bell can make thirds place. This causes the two bells behind to dodge together, but it will be in the 4–5 positions instead of the 3–4 positions (Table 6). The result is that whereas Plain Bob on four bells produces the sequence seconds, 3–4 down and 3–4 up, everything now moves one position further along to give thirds, 4–5 down and 4–5 up. Using this double hunt system, but otherwise proceeding as for Plain Bob, a plain course of Grandsire Doubles is produced as in Table 7. Touches are obtained by the use of bobs and singles having the effect of changing the second hunt bell and thus producing different changes. Like Plain Bob, Grandsire can be rung on all numbers of bells. Grandsire Triples, for example, is based on the same principle, being Plain Bob Minor (six bells) with an additional bell in the hunt.

So far the methods considered have been based on a lead with the treble having a plain hunting path. There is another and very large class of method where the treble has a dodging path instead of a plain one. An old word for dodging was ‘bobbing’, hence this path of the treble is called ‘treble bob’ and methods based on this dodging path are sometimes called treble bob methods. Other methods of this class are called ‘surprise’ or ‘delight’ methods. Whereas in plain hunt all the bells can do the same work and will come back to rounds without repetition, the bells cannot all have a dodging hunt because, as Table 8 shows, each change will be repeated. To avoid this, some alterations to treble bob hunting must be made, and the nature of these variations determines the particular method that is obtained. Table 9 gives the first leads of the two most-rung treble bob methods – here on six bells. Repetition is avoided by the bells in thirds and fourths place ‘making places’ (i.e. ringing two consecutive blows there) shortly before and after the lead ends, and another bell repeatedly making seconds throughout the middle of the lead.

These methods are considered relatively straightforward to ring, but there are many thousands of extremely of complex methods on the same basic plan of the treble following a treble bob path, but with the other bells making places in various parts of the lead. Table 10 gives the first leads of two of the most complex six-bell methods currently rung. Avoiding falseness when composing for treble dodging methods is extremely difficult and most composers now check their compositions by computer.

A method in which all the bells do the same work in a plain course is sometimes known as a ‘principle’, and the most popular principle is ‘Stedman’, composed by Fabian Stedman, the 17th-century ringer and writer. Plain hunt on three bells produces six changes, and these can be achieved in two different ways, known as forward and backward hunting (see Table 11).

For Stedman Doubles, the three bells at the front of the row ring plain hunt while the two bells in the 4–5 places dodge with each other. At the end of the six changes (known as a ‘six’), the bell in thirds place changes places with the bell in fourths place. Another six changes are rung on the new front three bells (two already there with one new one) while the two bells now at the back dodge with each other. The sixes (i.e. the sets of three bells hunting at the front) must, however, consist of alternate forward and backward hunting. The forward hunting six is known as a ‘quick six’ and backward hunting six as a ‘slow six’, and the plain course starts in the middle of a quick six. Table 12 gives a plain course of Stedman Doubles. After the first two changes bell no.4 goes into the front three places and stays there for 30 changes before going out to the back again. During those changes it follows what seems to the beginner a rather complicated path. Then after two sixes in the 4–5 places it goes into the front again, but after only six changes it comes straight out to dodge again in 4–5. These two pieces of work in the front are called ‘the slow’ and ‘the quick’ respectively.