(Fr. cadence; Ger. Kadenz, Schluss; It. cadenza).
The conclusion to a phrase, movement or piece based on a recognizable melodic formula, harmonic progression or dissonance resolution; the formula on which such a conclusion is based. The cadence is the most effective way of establishing or affirming the tonality – or, in its broadest sense, modality – of an entire work or the smallest section thereof; it may be said to contain the essence of the melodic (including rhythmic) and harmonic movement, hence of the musical language, that characterizes the style to which it belongs. The term was also used in France to denote various types of trill (also known as tremblement) or turn (double cadence); see Ornaments, §8.
W.S. ROCKSTRO, GEORGE DYSON/WILLIAM DRABKIN, HAROLD S. POWERS/JULIAN RUSHTON
In music of the tonal periods (Baroque, Classical and Romantic), it is useful to distinguish between cadences on the basis of their varying degrees of ‘finality’, for example between those whose final chord is on the tonic and those whose final chord is on some other degree of the scale, between those whose chords are all in root position and those which contain at least one inverted chord, and so on. A number of terms have been borrowed from medieval modal theory (authentic, plagal, Phrygian), not always on a strictly logical basis; there are also some cadences to which a number of names have been applied as a result of the persistence of terms introduced by theorists from the 18th century or earlier, and the translation of foreign-language equivalents. The following discussion is intended to clarify the meaning of the most important of these names as they are now used.
A cadence is said to be ‘perfect’ if it consists of a tonic chord preceded by a dominant chord (V–I, normally both in root position); it is occasionally stipulated that the final chord must have the tonic in the highest part. This is also called an ‘authentic’, ‘final’ or ‘full’ cadence, or a ‘full close’ (Fr. cadence parfaite, cadence authentique; Ger. Ganzschluss, vollkommene Kadenz; It. cadenza perfetta, cadenza intera). The term ‘perfect cadence’ is extended in some theoretical writings (chiefly American) to include what is more commonly called a ‘plagal cadence’, one in which the tonic is preceded by the subdominant (IV–I) or a subdominant with added sixth (Fr. cadence plagale; Ger. plagale Kadenz, sometimes unvollkommene Kadenz; It. cadenza plagale). A cadence whose final chord is prepared by subdominant and dominant harmonies, as in ex.1, is sometimes called a ‘mixed’ cadence.
An ‘imperfect’ or ‘half’ cadence, ‘semi-cadence’ or ‘half close’ (Fr. cadence suspendue; Ger. Halbschluss; It. cadenza sospesa) ends on the dominant and may be preceded by any chord. The simple succession I–V (ex.2) is common; so are IIb–V and IV–V. The expressive qualities of the imperfect cadence are illustrated in ex.3; within the space of seven bars of an aria there are three imperfect cadences, each of which is approached by a different chord. In American usage, ‘imperfect’ is sometimes applied to cadences ending on the tonic whose chords are not in root position (also known as ‘medial’ or ‘inverted’ cadences), or whose upper parts do not end on the tonic; only the terms ‘half cadence’ and ‘semi-cadence’ have the restricted meaning of an ending on the dominant.
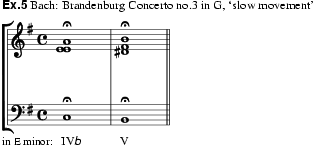
Related to the imperfect cadence is the Phrygian cadence, which is characterized by a diatonic approach to the final chord from an ‘upper leading note’ (i.e. the second degree of the scale when it lies only a semitone above the tonic). The more complicated – and more customary – use of this cadence in 16th-century polyphony is illustrated by the ending of Palestrina’s Jubilate Deo omnis terra (no.13 of the Offertoria of 1593). Ex.4a shows the cadential parts alone, with the ‘upper leading note’ in the tenor and the required suspension in the highest part. In ex.4b the other parts are also shown; as the two cadential voices approach the octave e–e' the bass must move down to A (or c) to avoid consecutive octaves with the highest part. In the final resolution on e, the motion of the bass, if described in tonal terms, resembles that of the plagal cadence (see above). In its simpler, more direct form, the Phrygian cadence has the upper leading note and its resolution in the lowest part. The chord progression shown in ex.5, which takes the place of a slow movement in Bach’s Brandenburg Concerto no.3 in G, is one of the many features of Renaissance compositional technique that survived in the Baroque era; but in this context it is better to interpret it as an imperfect cadence in E minor (the relative key of G major).
In an ‘interrupted’ cadence, also known as a ‘deceptive’ cadence or ‘false close’ (Fr. cadence rompue, cadence évitée, cadence trompeuse; Ger. Trugschluss; It. inganno), the penultimate chord, a dominant or dominant 7th, resolves irregularly, to some other chord than the tonic. This is most often the submediant, but sometimes the flattened submediant, the subdominant (usually in first inversion), the mediant (often with raised 3rd) or occasionally the tonic with an added flat 7th (i.e. a dominant 7th of the subdominant key). In Handel’s Fugue in B minor for organ, the final cadence, shown in ex.6, is ‘interrupted’ by a subdominant chord with an added 6th. In later music, particularly Wagner’s, the most common interrupting chord is the first inversion of sharp subdominant (which may imply the dominant of the dominant); this also occurs in Haydn.
American usage distinguishes a medial cadence, whose penultimate chord is inverted, from a radical cadence, whose chords are in root position. In the medial cadences given in ex.7, (a) and (b) are derived from the perfect (authentic) cadence in C major, (c) and (d) from the plagal cadence. The term ‘medial cadence’ is also sometimes applied to endings in plainchant and modal polyphony that are not on the final of the mode.
Whereas the notion of cadence in tonal music almost invariably implies harmonic resolution (either from the dominant or towards the tonic or dominant), until the 16th century cadences in polyphony were governed entirely by linear considerations, primarily the descent by step to the final of the prevailing mode, and secondarily the ascent by step to the final or the octave above the final; often motion by step was replaced by the leap of a 3rd. In Gregorian chant the ending most frequently used is descent by step to the final; the downward leap of a 3rd and ascent by a whole tone are also common. Ascent by a semitone, although possible in F-mode chants, is almost never found (the 13th-century Kyrie firmator sancte is exceptional in this respect), though ascent by a 3rd (d–f) occurs in rare instances (e.g. in the antiphon Vobis datum est). In the earliest forms of organum (11th–12th centuries) the primary cadences consisted of direct or indirect resolution of one perfect interval into another, namely a 4th or 5th into a unison or octave (ex.8). The secondary cadences consisted of the resolution of an imperfect interval into a perfect interval (i.e. the 3rd into a unison and the 6th into an octave); these became the principal endings in two-part polyphony in the 13th century. From about 1300 practically all cadences were based on the descent by step of the tenor, with the resolution of the other parts dependent on the interval each made with the tenor: the minor 3rd below normally resolved to the unison, the major 3rd above to the 5th, and the major 6th above to the octave (at cadence points, any major 3rds below or minor 3rds and 6ths above would be sharpened in performance; see Musica ficta). This produced a number of possible cadences in three parts, including the Phrygian cadence (ex.9a), the so-called ‘double leading note cadence’ (exx. 9b–c) and a cadence that contained consecutive 5ths (ex.9d); from the mid-14th century the Landini cadence (ex.9e), whose upper part characteristically falls to the sixth degree before rising to the octave, became the most important variant of the ‘double leading note cadence’.
The earliest apparent precedents for triadic harmony occur in certain types of cadential formulation prevalent in the 15th century. The movement of the principal parts, the cantus and tenor, was still governed by the linear resolution of intervals (now usually preceded by a dissonant suspension), but the contratenor moved by leap more often than before. The configurations in ex.10, all commonly found in music from Du Fay to Josquin, seem to anticipate the perfect candence when viewed ‘vertically’, that is, as successions of chords (see Randel). However, in linear terms (see Bent) they are essentially no different from the progressions in ex.9, since from a theoretical point of view they were still based on the tenor part; as late as 1529 the progression in ex.11 was described by Aaron in Thoscanello de la musica as a cadence on E. An important contribution to cadence formation in the Renaissance was the addition of the 3rd in the final chord; until about 1750 it was normally sharpened in minor-mode compositions, so that almost all pieces ended on a major triad (see Tierce de Picardie).
Even in late Renaissance theory, cadences were still viewed as contrapuntal or melodic occurrences; for Zarlino (Le istitutioni harmoniche, 1558) the cadenza perfetta was the resolution of two parts to the octave, and the cadenza imperfetta (sfuggita) the resolution to the 3rd (10th) or 5th (12th). Early in the 18th century the distinction between cadences on the tonic and on other degrees, as well as between perfect and plagal, was made on the basis of harmonic progression; the notion of an interrupted cadence was also introduced at this time. In France the perfect cadence was called a cadence parfaite, the plagal a cadence imparfaite (Rameau used the term cadence irregulière); in Germany vollkommene Cadenz and Ganzschluss were used for the perfect cadence, unvollkommene Cadenz, Halbschluss (or halbe Cadenz) and Trugschluss for plagal, imperfect and interrupted cadences. Rameau postulated that a cadence consisted in the resolution of a ‘characteristic dissonance’ present or implied in the penultimate chord. If the characteristic dissonance lay a 7th above the real bass, its resolution was called a cadence parfaite (ex.12a); if it lay a 6th above (‘sixte ajoutée’; see Added sixth chord), its resolution was called a cadence irregulière (ex.12b). Thus the progression I–IV–I–V–I, according to Rameau, would be analysed as a series of cadences parfaites (I–IV and V–I) and cadences irregulières (IV–I and I–V), that is, independently of a larger tonal function (the bracketed pairs of notes in ex.12c are the imagined characteristic dissonances together with their respective resolutions).
In Classical music, which is built to a great extent on the principle of antecedent and consequent phrases, cadences took on a structural significance on all levels of composition. Moreover, cadence formations became so standardized that they could be used, for rhetorical effect, even in positions other than endings. In some of Haydn’s quartets, for instance, a homophonic cadential progression is stated at the very beginning of the first movement (ex.13). The trio section from the minuet of Mozart’s ‘Jupiter’ Symphony (ex.14) begins with a perfect cadence answered by a contrapuntal passage, thus reversing the normal roles of ‘activity’ and ‘repose’ within a phrase. In the opening of Beethoven’s Symphony no.1 (ex.15) the first two chords could be heard initially as a perfect cadence in F, until the next two chords are played; these, in turn, can be analysed as an interrupted cadence whose ‘resolution’ takes the form of an imperfect cadence in the third pair of chords.
The
expansion of the sonata in 19th-century instrumental music, and especially the
development of musical continuity in German Romantic opera (Wagner’s
‘unendliche Melodie’), brought to the interrupted cadence a structural
significance that had hitherto been the exclusive property of the perfect and
imperfect cadences (ex.16). By contrast Richard Strauss, whose opera acts and tone
poems were through-composed but were nevertheless subdivided by cadence-points,
developed a kind of counterpart to the interrupted cadence, in which the
penultimate dominant 7th was replaced, or separated from the tonic, by some
other chord (ex.17). Resistence to the clear V–I
is common in this period, in the works of composers as diverse as Elgar and
Debussy. In a composition foreshadowing atonality, the final movement of his
String Quartet no.2, op.10, Schoenberg prolonged a dominant (C
) harmony (bars 128–133) but
resolved it obliquely on to C major; the approach to the final tonic, 20 bars
on, is similarly indirect (ex.18).
The development of cadences in the 20th century was a matter of embellishment rather than of inherent structural change; in the cadences of post-tonal composers such as Stravinsky and Hindemith there was a return to the principle of linear progression in all parts (ex.19). Stravinsky’s chorale-endings similarly depend on a linear approach to the final resting-place, with the last chord a clearly-voiced dissonance (Symphonies of Wind Instruments). Music based on repetitive patterns may end by breaking the pattern, a favourite device of Stravinsky (as in The Rite of Spring).
In
rigorously non-tonal music the principles of suspension, resolution, functional
harmonic progression and even melodic formula may no longer apply and the sense
of an ending is instead achieved through rhythm, dynamics and other variables
such as instrumentation. Some 12-note compositions nevertheless contrive to end
on a triad (Schoenberg’s Ode to Napoleon) or a clearly voiced harmony
(Schoenberg’s Piano Concerto). Each of these endings is an emphatic tutti, with
ritardando; similar rhetorical means are employed in Schoenberg’s Variations
for Orchestra, op.31, whose last chord contains eleven pitches (lacking only C
, which is sounded alone
as a penultimate). Quiet endings also provided ways of avoiding cadential
formulae. In Mahler’s Ninth Symphony the etiolated plagal cadence contributes
less to finality than do harmonic immobility, texture and the incursion of
silence; with less orthodox harmony, the celebrated ending of ‘Neptune’ in
Holst’s The Planets employs an alternation of unconventionally related
chords fading into inaudibility (ex.20). An atonal
example of similar rhetorical character is Boulez’s Le marteau sans maître.
Grove6
A. Casella: L’evoluzione della musica a traverso la storia della cadenza perfetta (London, 1924; Eng. trans., 1924, rev. 2/1964 by E. Rubbra)
R. Tenschert: ‘Die Kadenzbehandlung bei Richard Strauss: ein Beitrag zur neueren Harmonik’, ZMw, viii (1925–6), 161–71
C.L. Cudworth: ‘Cadence galante: the Story of a Cliché’, MMR, lxxix (1949), 176–82
M.E. Brockhoff: ‘Die Kadenz bei Josquin’, IMSCR V: Utrecht 1952, 86–95
D. Schjelderup-Ebbe: Purcell’s Cadences (Oslo, 1962)
F.W. Homan: ‘Final and Internal Cadential Patterns in Gregorian Chant’, JAMS, xvii (1964), 66–77
S.H. Hansell: ‘The Cadence in 18th-Century Recitative’, MQ, liv (1968), 228–48
D.M. Randel: ‘Emerging Triadic Tonality in the Fifteenth Century’, MQ, lvii (1971), 73–86
D. Venus: ‘Zum Problem der Schlussbildung im Liedwerk von Schönberg, Berg und Webern’, Musik und Bildung, iv (1972), 117–23
R. Eberlein: Kadenzwahrnehmung und Kadenzgeschichte: ein Beitrag zu einer Grammatik der Musik (Frankfurt, 1992)
J. Schmalfeldt: ‘Cadential Process: the Evaded Cadence and the “One More Time” Technique’, JMR, xii (1992), 1–52
Z. Eitan: ‘Functionality within Cluster Harmony: Cadences and Primary Notes in the First Movement of Ligeti’s Double Concerto (1972)’, Orbis musicae, xi (1993–4), 92–123
C. Thorau: ‘Der Trugschluss und das Ende der Rhetorik: John Cages “Lecture on Nothing” aus rhetorischer Sicht’, Zeichen am Weg: eine Sämmlung von Aufsätzen zum 65. Geburtstag von Heinrich Poos (Berlin, 1994), 79–86
M. Bent: ‘The Grammar of Early Music: Preconditions for Analysis’,Tonal Structures in Early Music, ed. C. Judd (New York, 1998), 15–59