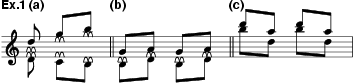Harmonics.

Sets of musical notes whose frequencies are related by simple whole number ratios. A harmonic series is a set of frequencies which are successive integer multiples of the fundamental (or first harmonic). For example, the set of frequencies 100, 200, 300, 400, 500 Hz … is a harmonic series whose fundamental is 100 Hz and whose fifth harmonic is 500 Hz. In general, the nth harmonic of a series has a frequency which is n times the fundamental frequency.

1. General.

The importance of harmonics in various branches of music theory and practice derives ultimately from the way in which sound is perceived by the human ear and brain. The pressure fluctuations at the eardrum of a listener, which give rise to the sensation of sound (musical or otherwise), normally have a complex pattern or waveform. In 1822 the French mathematician Fourier showed that any waveform, however complex, could be decomposed into a set of simple sine wave components. If the waveform is periodic, corresponding to a regularly repeating pattern of pressure variation, then its sine wave components are members of a harmonic series. In this case it is difficult to perceive the components separately; they are fused into a single sound with a definite musical pitch. In contrast, a sound which has a set of components which are not harmonics (or close approximations to harmonics) will not normally be perceived as having a clear pitch, and the components can be heard separately. The pitch associated with a harmonic series is that of the fundamental or first harmonic; the frequency spectrum, which describes the relative strengths of the frequency components, helps to determine the timbre of the note, with an increase in the strength of upper harmonics giving an increased brightness to the sound.

The 19th-century acoustician Helmholtz developed a theory which related the dissonance of a musical interval to the degree of beating between the harmonics of the different notes forming the interval. Notes whose fundamental frequencies are related by small whole number ratios have reduced beating because of coincidences between the frequencies of the harmonics concerned (see Interval); this may at least partially explain why several of the intervals between successive members of the harmonic series are of great importance in Western music. The intervals between the first 25 harmonics, to the nearest cent, are shown in Table 1, which also gives the pitches of the harmonics for a series whose fundamental pitch is C.

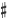2. Wind instruments.

A wind instrument, conventionally blown, generates a continuous pitched note corresponding to a periodic waveform and a harmonic set of frequency components. Usually several different pitches can be obtained for a fixed pattern of fingering or valve depression; these pitches are described as the natural notes of the instrument. The fundamental frequency of a natural note is determined by a complex interaction between the tone generator (air jet, reed or lips) and the air column of the instrument (see Acoustics, §IV).

In most wind instruments, the air column has a series of resonances whose frequencies are close to being members of a harmonic series. It is important to realize, however, that in real wind instruments the air column resonances are never perfectly harmonic. The fundamental frequency of the sounded note is usually close to one of the air column resonances; to move from one resonance to another the player modifies the tone generator (for example, by changing the lip pressure on a reed), sometimes also opening a register key to modify the air column. When a new air column resonance has been selected, a new note is established, for which the fundamental frequency is close to the new air column resonance. Associated with the new note will be an exactly harmonic set of frequency components, since the new vibration pattern is periodic; but whether the interval between the new note and the old corresponds to an exactly harmonic interval will depend on the skill with which the instrument maker tuned the air column resonances, and the extent to which the player ‘pulls’ the note by adjusting the method of blowing.

Despite the fact that the natural notes obtained in the way described above are not necessarily exact harmonics, the term ‘harmonic’ is customarily used as a synonym for ‘natural note’, and this usage will be followed in the remainder of the article. On the flute, the second air column resonance is approximately an octave above the first, so that an octave harmonic can be obtained; subtle adjustment of blowing pressure and angle can correct the intonation as required. On the clarinet the second air column resonance frequency is approximately three times that of the first, so the second register is a 12th above the first, corresponding to the third harmonic. In the harmonic flute organ pipe, a small hole is bored approximately half way along the tube, at a point which is a pressure antinode for the first resonance of the air column. This effectively kills the first resonance, encouraging the pipe to sound at the second harmonic, an octave above the first.

On brass instruments, with their longer and narrower tubes, a greater number of harmonics is obtained by tightening the lips; these harmonics provide the only basic notes on the natural (i.e. slideless, keyless and valveless) trumpet and horn. Bach regularly wrote for the trumpet notes between the 3rd and 18th harmonics and once, in Cantata no.31, wrote for the 20th harmonic. Mozart wrote for the horn from the 2nd harmonic to the 24th (12 Duos for two horns k487/496a).

It can be seen from Table 1 that harmonics which are multiples of prime numbers above 5 (e.g. nos.7, 11, 13 and 14) do not correspond to recognized notes in the equal-tempered scale. However, on a C trumpet nos.7 and 14 can fairly easily be lipped up to b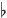, and skilled trumpeters can lip no.11 down to f'' or up to f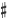'' and no.13 up to a''; composers regularly wrote these notes. Some trumpeters were more skilled at this than others, as can be seen in the writings of 18th-century music historians. The problem was solved by means of hand-stopping on the horn and the use of a slide on the trumpet, before the invention of valves made it unnecessary to use these particular harmonics. Harmonics nos.17 and 19 are good approximations of c''' and d''', but composers do not seem to have used them.

The timbral effects of harmonics have long been used in organ building. Although organ pipes possess a wide harmonic range, the effect can be heightened without forcing by adding further pipes whose fundamentals are the harmonics of the foundation or ‘diapason’ ranks. Since the 15th century these extra ranks have been made to draw separately, and the organist can synthesize a variety of tone qualities by combining stops corresponding to the 1st to 6th harmonics and compound stops of pre-set combinations of harmonics such as nos.6, 8, 12 and 16 (Mixture), 3, 4 and 5 (Cornet), 3 and 5 (Sesquialtera) or even occasionally 5, 6, 7 and 8 (‘harmonics’). Harmonics nos.1, 3 and 5 on flute-toned stops, for example, synthesize quite a good imitation of a clarinet. Some keyboard Electronic instruments also use this principle to synthesize various tone-colours, a technique known as additive synthesis. For further discussion of the acoustical basis of harmonics see Sound, §6(ii).

3. Strings.

It was noted in the previous section that the resonance frequencies of the air column in a real wind instrument are never exact harmonics; the same is true of the resonance frequencies of a real musical instrument string. An ideal, completely flexible string with absolutely rigid supports would have an exactly harmonic set of resonances; in practice these conditions are never met, and the resonance frequencies are usually slightly further apart than a true harmonic series (see Inharmonicity). This results in an interesting distinction between plucked and bowed notes. Bowing a string in the normal manner gives a periodic vibration of the string, and the sound therefore has a frequency spectrum containing exact harmonics (neglecting some minor transient effects). When a string is plucked or struck, in contrast, each resonance of the string radiates sound at its own frequency, giving a slightly inharmonic frequency spectrum. The inharmonicity is usually negligible for violin and guitar strings, but is of considerable significance in pianos.

A bowed string normally vibrates at a frequency very close to that of the first string resonance. The mode of vibration corresponding to this resonance has a displacement antinode (point of maximum amplitude of vibration) at the centre of the string. Touching the string lightly at this point kills the vibration of the first mode, but leaves the second mode unscathed, since it has a node at the centre; the string then establishes a new vibration pattern, with a vibration frequency corresponding to the second string resonance. Neglecting the very small inharmonicity of the string resonances, this new note is described as the second harmonic of the string.

Upper harmonics are often used for special effects on string instruments and on the harp. In the violin family, the use of harmonics of open strings, ‘natural’ harmonics (‘flageolet tones’), was introduced by Mondonville in Les sons harmoniques: sonates à violon seul avec la basse continue op.4 (c1738). In his preface he explained how to obtain harmonics nos.2, 3, 4, 5, 6, 8 and above by lightly fingering at a node on any string. The sonatas make considerable use of harmonics nos.2, 3, 4 and 5. For the 2nd harmonic, the note is fingered in its normal position but only lightly. For the 3rd, 4th and 5th harmonics, the player fingers lightly as if to play a perfect 5th, 4th or major 3rd above the open string (or at other nodal points: at any multiple of an nth of the distance along the string for an nth harmonic); harmonics sounding a 12th, two octaves and a 17th above the open string are obtained. In ex.1a the special sign above each notehead indicates that the player fingers in the positions of the lower notes on the g string and the upper notes (only) are sounded. The passage in ex.1b sounds as in ex.1c, assuming that both written notes are played as harmonics, the upper line on the d' string and the lower on the g. Mondonville also used 2nd (octave) harmonics on the G and d strings of the cello in the same sonatas. In modern notation there is either a small circle over the actual note or a diamond-headed note in the position of the nodal point to be touched (e.g. Ravel: Ma mère l’oye).

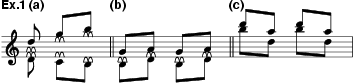
The most commonly used ‘artificial’ harmonics are 4th harmonics of the written fingered notes, which sound two octaves above those notes; they are obtained by fingering the written note and lightly touching the string a perfect 4th above, and are notated by writing diamond-headed notes a perfect 4th above the main note.

With a long string strongly bowed as many harmonics may be obtained as on the trumpet. This was the principle of the one-string Trumpet marine, which could play trumpet music with a characteristic out-of-tune effect on the 4th and 6th of the scale.

On the harp 2nd harmonics, sounding one octave above, are obtained by plucking the upper half of the string with the side of the thumb and lightly touching the mid-point of the string with the ball of the thumb. Harp harmonics are designated by a small circle above the written normal note of the string.

BIBLIOGRAPHY

H.L.F. Helmholtz: Die Lehre von den Tonempfindungen (Brunswick, 1863, 4/1877; Eng. trans., 1875, 2/1885/R, 6/1948, as On the Sensations of Tone)

C.A. Taylor: The Physics of Musical Sounds (London, 1965)

A.H. Benade: Fundamentals of Musical Acoustics (New York, 1976, 2/1990)

M. Campbell and C. Greated: The Musician’s Guide to Acoustics (London, 1987/R)

N.H. Fletcher and T.D. Rossing: The Physics of Musical Instruments (New York, 1991, 2/1998)

GUY OLDHAM/MURRAY CAMPBELL, C. GREATED