Degree.

The position of a note with reference to a scale, sometimes called a scale-step (see Stufe); the referential scale is usually assumed to be diatonic (i.e. a major or minor scale or one of the church modes). Degrees may be defined in terms of their melodic or harmonic function; that is, a melody can be described as movement from one degree to another, and harmony can be analysed by the succession of degrees in the lowest voice of a polyphonic texture or by the succession of degrees that constitute the roots of the chords which make up that texture. In harmonic analysis the degrees are most often identified by roman numerals, from I to VII. In melodic analysis no system of naming the degrees has been universally accepted, though Schenker’s notation with capped arabic numerals (1, 2, 3 etc.) has gained some currency.

Notes that do not belong to the referential scale can nevertheless be described in terms of it. In C major, for instance, F is the raised fourth degree, B the lower (or flattened) seventh. This method of description can be applied to the notation for harmonic and melodic degrees given above (e.g. IV, 7).

The first degree of the scale is called the tonic; this is the note by which the referential scale is named. In tonal music, the next most important degree is the fifth or dominant, and the tonic and dominant may often be regarded as mutually complementary. The fourth degree is the subdominant – the inversion of the dominant, or the note to which the tonic acts as dominant. The other degrees are as follows: second, supertonic (this is the dominant of the dominant; see Applied dominant); third, mediant; sixth, submediant; and seventh, leading note (ex.1).

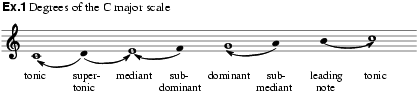
WILLIAM DRABKIN