In part-writing, the simultaneous duplication of the melodic line of one part by another at the interval of a perfect 5th (ex.1a) or an octave (ex.1b), or any equivalent compound interval.
In the earliest stages of polyphony, from the 11th century to the 13th, only the unison, the 5th and the octave were regarded as true consonances to be used at cadences and other strong points of articulation. Consecutive 5ths were common in organum and in conductus-style pieces such as the anonymous three-part motet whose incipit is quoted in ex.2 (GMB, no.18). The first theorist to prohibit them was Johannes de Grocheo (Optima introductio in contrapunctum, c1300; CoussemakerS, iii, 12), who forbade consecutive perfect consonances of the same size between two parts of a composition. Nevertheless, consecutive 5ths were used frequently in 14th-century three-part writing, and after 1400 can occasionally be found between two parts of a piece whose contrapuntal design is built on a third part (i.e. the tenor), for instance in the three-part cadence on the scale degrees 1–8–12 instead of the normal 1–5–8 (ex.3). From the high Renaissance on, theorists generally forbade the use of consecutive 5ths and octaves in strict counterpoint, and their occurrence in music up to the late 19th century was incidental.
The argument most often advanced against the use of consecutive octaves is that it eliminates one of the parts of a contrapuntal texture in an inartistic way, that is by doubling another. In the case of consecutive 5ths this argument does not apply, since a different set of notes is present in each part. Cherubini’s argument against consecutive 5ths was that one would not know on which part to base the tonality of a two-part passage in consecutive 5ths (Cours de contrepoint et fugue, 1835–6); this view was repeated 100 years later by Schenker, whose made-up examples of consecutive 5ths in Der freie Satz (ex.4) present an amusing case against their use. It is now thought that consecutive 5ths were avoided on ‘aesthetic’ grounds, namely that the bareness of the interval of a 5th is accentuated when it leads immediately to another 5th; this argument can account for the objection to simple pairs of consecutive 5ths better than the theory of doubtful tonality advanced by Cherubini and Schenker, and it can also explain further the objection to consecutive octaves.
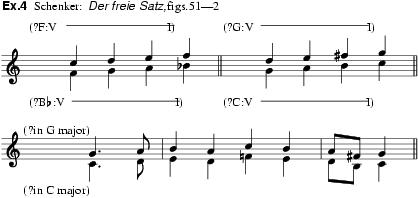
When
consecutive 5ths and octaves do occur in tonal music, a non-harmonic note or an
ornament is usually present. In ex.5 an octave is approached from an
augmented octave; the grace note b
'' in the first violin part is for expressive
effect and not part of the contrapuntal design. In ex.6 consecutive 5ths are made by the auxiliary note d
'' on the downbeat.
Consecutive 5ths are often caused by appoggiaturas or accented passing notes in
one part (exx.7–8). A special type of consecutive 5ths,
called ‘Mozart’ 5ths (Ger. Mozartquinten), occurs when the German 6th
chord resolves directly to the dominant (ex.9); examples in Mozart, however, are rare, as he normally
modified the part-writing in such harmonic progressions so as to avoid
consecutives. A number of instances of consecutives in Classical and Romantic
music have been known to be ‘corrected’ by over-zealous editors: for example,
in the first movement of Beethoven’s ‘Harp’ Quartet (ex.10), the consecutive 19ths between e''–d'' in the first violin and A–G in the cello led
to the erroneous alteration of the cello’s G to F in some
editions.
In the late 19th century and the 20th, consecutive 5ths were used for exotic, folklike or archaic effect or as a means of ‘doubling’ a part at an interval other than an octave, for instance in Act III of Puccini’s La bohème.
A.W. Ambros: Zur Lehre von Quinten-Verbote (Leipzig, 1859)
F.E. Gladstone: ‘Consecutive Fifths’, PMA, viii (1881–2), 99–121
M.G. Sewall: ‘Hucbald, Schoenberg and Others on Parallel Octaves and Fifths’, MQ, xii (1926), 248–65
F.T. Arnold: ‘J.S. Bach and Consecutives in Accompaniment’, ML, xiv (1933), 318–25
M. Shirlaw: ‘Aesthetic – and Consecutive Fifths’, MR, x (1949), 89–96
J.W. Hill: ‘Realized Continuo Accompaniments from Florence c. 1600’, EMc, xi (1983), 194–208
G. Chew: ‘The Perfections of Modern Music: Consecutive Fifths and Tonal Coherence in Monteverdi’, MAn, viii (1989), 247–73
R.T. Laudon: ‘The Debate about Consecutive Fifths: a Context for Brahms’s Manuscript Oktaven und Quinten’, ML, lxxiii (1992), 48–61
See also Hidden fifths, hidden octaves.
WILLIAM DRABKIN